练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简，再求代数式的值，其中a=tan60°﹣6sin30°．


    【考点】分式的化简求值；特殊角的三角函数值．

    【专题】探究型．

    【分析】先根据分式混合运算的法则把原式进行化简，再由特殊角的三角函数值计算出a的值，把a的值代入进行计算即可．

    【解答】解：原式=÷

    =×

    =﹣，

    当a=tan60°﹣6sin30°=﹣6×=﹣3时，原式=﹣=﹣．

    【点评】本题考查的是分式的化简求值及特殊角的三角函数值，熟知分式混合运算的法则是解答此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    图中几何体的主视图为(     )

    A．    B．   C．   D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


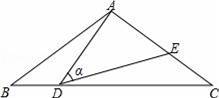
    如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B、C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=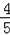，则线段CE的最大值为　　　　　　．

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，DE∥BC，分别交△ABC的边AB、AC于点D、E， =，若AE=5，则EC的长度为（　　）

    A．10     B．15     C．20     D．25

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从一副没有“大小王”的扑克牌中随机抽取一张点数为8的扑克，其概率是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


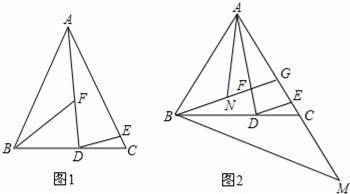
    如图1，在等腰三角形ABC中，AB=AC，在底边BC上取一点D，在边AC上取一点E，使AE=AD，连接DE，在∠ABD的内部作∠ABF=2∠EDC，交AD于点F．

    （1）求证：△ABF是等腰三角形；

    （2）如图2，BF的延长交AC于点G．若∠DAC=∠CBG，延长AC至点M，使GM=AB，连接BM，点N是BG的中点，连接AN，试判断线段AN、BM之间的数量关系，并证明你的结论．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直角三角形的两边长分别是6，8，则第三边的长为（　　）

    A．10     B．2  C．10或2       D．无法确定

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读下列材料，然后回答问题：

    在进行二次根式运算时，我们有时会碰上如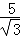、这样的式子，其实我们还可以将其进一步化简：；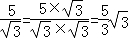

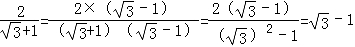    ．以上这种化简过程叫做分母有理化．

    还可以用以下方法化简：．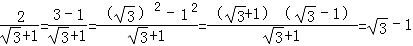

    （1）请用其中一种方法化简；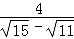

    （2）化简：．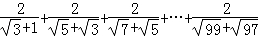

    查看答案和解析>>

    科目：初中数学 来源： 题型：


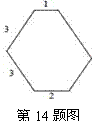
    一个六边形的六个内角都是120o（如图），连续四条边的长依次为 1,3,3,2，

    则这个六边形  的周长是(     )

    A. 13        B. 14         C. 15        D. 16

     


    查看答案和解析>>

    同步练习册答案