练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
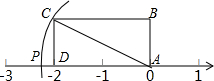
    4．如图，长方形ABCD的边AB=1，BC=2，AP=AC，则点P所表示的数是（　　）
    A．5B．-2.5C．$\sqrt{5}$D．$-\sqrt{5}$

    分析 根据勾股定理求出长方形ABCD的对角线AC的长，即为AP的长，进而求出点P所表示的数．

    解答 解：∵长方形ABCD的边AB=1，BC=2，
    ∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$，
    ∴AP=AC=$\sqrt{5}$，
    ∴点P所表示的数为-$\sqrt{5}$．
    故选D．

    点评 本题考查了实数与数轴，利用勾股定理求出长方形ABCD的对角线AC的长是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

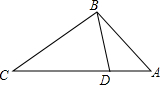    14．如图，点D在△ABC的边AC上，要判断△ADC与△ABC相似，添加一个条件，不正确的是（　　）
    A．∠ABD=∠CB．∠ADB=∠ABCC．CB2=CD•CAD．AB2=AD•AC

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

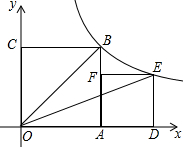    15．如图，两个正方形OABC、ADEF拼放于直角坐标系中，反比例函数y=$\frac{k}{x}（k≠0，x＞0）$的图象经过B点和E点，已知△OEB的面积为2，则正方形ADEF的面积为（　　）
    A．1B．6-2$\sqrt{5}$C．$\sqrt{5}-1$D．3$\sqrt{5}$-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知点A、B、C三个点在同一条直线上，若AB=3厘米，BC=2厘米，则线段AC的长为1或5厘米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知x=1，y=2是方程ax+y=5的一组解，则a的值是（　　）
    A．-3B．-2C．3D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）$\left\{\begin{array}{l}y=2x-3\\ x+2y=14\end{array}\right.$
    （2）$\left\{\begin{array}{l}{3x-y=-5}\\{2x+3y=4}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）一不透明纸箱中装有形状、大小、质地等完全相同的4个小球，分别标有数字1，2，3，4．
    ①从纸箱中随机地一次取出两个小球，求这两个小球上所标的数字一个是奇数另一个是偶数的概率；
    ②先从纸箱中随机地取出一个小球，用小球上所标的数字作为十位上的数字；将取出的小球放回后，再随机地取出一个小球，用小球上所标的数字作为个位上的数字，则组成的两位数恰好能被3整除的概率是多少？试用树状图或列表法加以说明．
    （2）如图，花丛中有一路灯杆AB．在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH=5米．如果小明的身高为1.7米，求路灯杆AB的高度（精确到0.1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

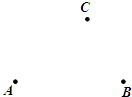    13．如图，已知点A、B、C，根据下列语句画图：（尺规作图，要保留作图痕迹．）
    （1）画出直线AB；
    （2）画出射线AC；
    （3）在线段AB的延长线上截取线段BD，使得AD=AB+BC；
    （4）画出线段CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．在Rt△ABC中，∠C=90°，cosB=$\frac{4}{5}$，AC=6，则△ABC的周长为24．

    查看答案和解析>>

    同步练习册答案