
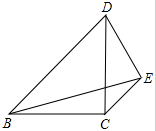
 如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.
如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$. 分析 作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,根据平行线的性质和已知条件得出四边形BNCM是正方形,设CM=BM=BN=CN=DN=a,根据BE=BD,得出BE=BD=2a,再根据勾股定理得出EM=$\sqrt{B{E}^{2}-B{M}^{2}}$=$\sqrt{3}$a,从而求出CE=EM-CM=($\sqrt{3}$-1)a,最后代入要求的式子即可得出答案.
解答 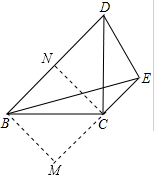 解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,
解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,
∵CE∥BD,
∴∠MCN=∠CND=90°,
∴四边形BNCM是矩形,
∵BC=CD,∠BCD=90°,
∴△BCD是等腰直角三角形,
∵CN⊥BD,
∴BN=DN=CN,
∴四边形BNCM是正方形,
设CM=BM=BN=CN=DN=a,
∵BE=BD,
则BE=BD=2a,
∴EM=$\sqrt{B{E}^{2}-B{M}^{2}}$=$\sqrt{3}$a,
∴CE=EM-CM=($\sqrt{3}$-1)a,
∴CE:BD=($\sqrt{3}$-1)a:2a=$\frac{\sqrt{3}-1}{2}$.
故答案为$\frac{\sqrt{3}-1}{2}$.
点评 本题考查了等腰直角三角形的判定与性质,平行线的性质,正方形的判定与性质,勾股定理,难度适中.关键是作出辅助线,求出四边形BNCM是正方形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:填空题
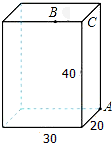 如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.
如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
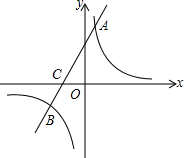 如图,在平面直角坐标系中,一次函数y=2x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).
如图,在平面直角坐标系中,一次函数y=2x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
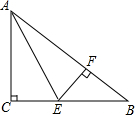 如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
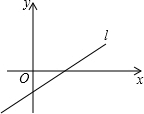 已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.
已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com