
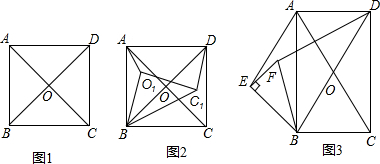
分析 (1)根据正方形的性质得AO=OC=OD,∠ODC=∠OCD=45°,∠DOC=90°,由勾股定理得到AO与CD之间的数量关系;
(2)如图2根据正方形的性质得AB=BC,AC=BD,OB=OC,∠OBC=∠ABO=45°,∠BOC=90°,得到△ABC和△OBC都是等腰直角三角形,求出AC=$\sqrt{2}$AB BC=$\sqrt{2}$BO,得到BD=$\sqrt{2}$AB,因为△BOC绕点B逆时针方向旋转得到△BO1C1,所以∠O1BC1=∠OBC=45°,OB=O1B,BC1=BC,BC1=$\sqrt{2}$BO1,由∠1+∠3=45°,∠2+∠3=45°,得到∠1=∠2,于是得到△BDC1∽△BAO1,求出结论;
(3)如图3在Rt△ABD中,cos∠ABD=$\frac{AB}{BD}$,在Rt△EBF中,cos∠EBF=$\frac{EB}{FB}$因为∠EBF=∠ABD=30°得到$\frac{BE}{BF}$=$\frac{AD}{BD}$=$\frac{\sqrt{3}}{2}$,再由∠EBF+∠FBA=∠ABD+∠FBA,得到
∠EBA=∠FBD,△AEB∽△FBD,由相似的性质得到解.
解答 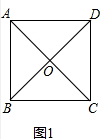 解:(1)AO=$\frac{\sqrt{2}}{2}$CD.理由如下:如图1,
解:(1)AO=$\frac{\sqrt{2}}{2}$CD.理由如下:如图1,
∵四边形ABCD为正方形,
∴AO=OC=OD,∠ODC=∠OCD=45°,∠DOC=90°,
∴AO=CO=$\frac{\sqrt{2}}{2}$CD,
故答案为AO=$\frac{\sqrt{2}}{2}$CD;
(2)如图2,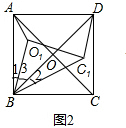
∵四边形ABCD为正方形,
∴AB=BC,AC=BD,OB=OC,∠OBC=∠ABO=45°,∠BOC=90°,
∴△ABC和△OBC都是等腰直角三角形,
∴$AC=\sqrt{2}AB,BC=\sqrt{2}BO$,
∴$BD=\sqrt{2}AB$,
∵△BOC绕点B逆时针方向旋转得到△BO1C1,
∴∠O1BC1=∠OBC=45°,OB=O1B,BC1=BC,
∴BC1=$\sqrt{2}$BO1,
∵∠1+∠3=45°,∠2+∠3=45°,
∴∠1=∠2,
∴△BDC1∽△BAO1,
∴$\frac{{DC}_{1}}{{AO}_{1}}=\frac{BD}{BA}=\sqrt{2}$,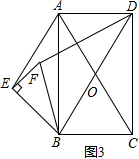
∴${AO}_{1}=\frac{\sqrt{2}}{2}{DC}_{1}$;
(3)如图3 在Rt△EBF中,cos∠EBF=$\frac{EB}{FB}$
在Rt△ABD中,cos∠ABD=$\frac{AB}{BD}$,
∵∠EBF=∠ABD=30°,
∴$\frac{BE}{BF}$=$\frac{AD}{BD}$=$\frac{\sqrt{3}}{2}$,
∵∠EBF+∠FBA=∠ABD+∠FBA,
即∠EBA=∠FBD,
∴△AEB∽△FBD,
∴$\frac{AE}{DF}$=$\frac{\sqrt{3}}{2}$,
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,旋转的性质,相似三角形的性质与判定等知识点,找相似三角形是关键.


科目:初中数学 来源: 题型:填空题
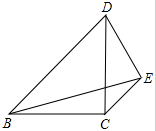 如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.
如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com