
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB. 
(1)若PF=PB,求证:PB是⊙O的切线;
(2)如果AB=10,BC=6,求CE的长度.
【答案】
(1)证明:∵PF=PB,
∴∠PFB=∠PBF,
又∵∠DFE=∠PFB,
∴∠DFE=∠PBF,
∵AB是圆的直径,
∴∠ACB=90°,即AC⊥BC.
又∵OD∥BC,
∴OD⊥AC.
∴在直角△DEF中,∠D+∠DFE=90°,
又∵OD=OB,
∴∠D=∠DBO,
∴∠DBO+∠PBE=90°,即PB⊥AB,
∴PB是⊙O的切线;
(2)解:∵OD∥BC,OA=OB,
∴OE= ![]() BC=
BC= ![]() ×6=3.
×6=3.
∵OD⊥AB,
∴EC=AE.
∵在直角△OAE中,OA= ![]() AB=
AB= ![]() ×10=5,
×10=5,
∴AE= ![]() =
= ![]() =4.
=4.
∴EC=4.
【解析】(1)根据等边对等角以及对顶角相等可以证得∠DFE=∠PBF,∠D=∠DBO,然后根据圆周角定理证明△DEF是直角三角形,据此即可证得∠PBA=90°,从而证明PB是切线;(2)根据三角形的中位线定理求得OE的长,然后根据垂径定理即可求解.
【考点精析】通过灵活运用切线的判定定理,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.


科目:初中数学 来源: 题型:
【题目】太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=75cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是 cm.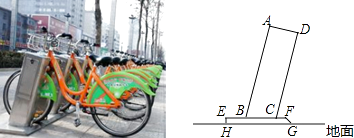
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小峰家要在一面长为38m的墙的一侧修建4个同样大小的猪圈,并在如图所示的5处各留1.5m宽的门,已知现有的材料共可修建长为41m的墙体,则能修建的4个猪圈的最大面积为 . 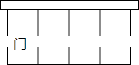
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字﹣1,2,5,;乙袋中装有3个完全相同的小球,分别标有数字3,﹣5,﹣7;小宇从甲袋中随机摸出一个小球,记下数字为m,小惠从乙袋中随机摸出一个小球,记下的数字为n.
(1)若点Q的坐标为(m,n),求点Q在第四象限的概率;
(2)已知关于x的一元二次方程2x2+mx+n=0,求该方程有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x﹣6与x轴交于点A(﹣6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.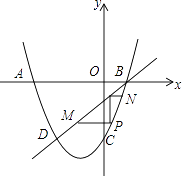
(1)连接CD,求抛物线的表达式和线段CD的长度;
(2)在线段BD下方的抛物线上有一点P,过点P作PM∥x轴,PN∥y轴,分别交BD于点M,N.当△MPN的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处(如图1).
(1)如图2,设折痕与边BC交于点O,连接,OP、OA.已知△OCP与△PDA的面积比为1:4,求边AB的长;
(2)动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN、CA,交于点F,过点M作ME⊥BP于点E.
①在图1中画出图形;
②在△OCP与△PDA的面积比为1:4不变的情况下,试问动点M、N在移动的过程中,线段EF的长度是否发生变化?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com