Question

直线y=kx-4与y轴的夹角为α，且tanα=

1

2

，则k=

 

．

Answer 1

考点：解直角三角形,一次函数图象上点的坐标特征

专题：计算题

分析：直线y=kx-4与y轴交于点B，与x轴交于点A，如图，则B（0，-4），在Rt△AOB中，根据正切的定义可计算出OA=

1

2

OB=2，则A点坐标为（2，0）或（-2，0），然后把（2，0）或（-2，0）分别代入y=kx-4可计算出相应的k的值．

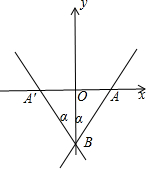
解答：解：直线y=kx-4与y轴交于点B，与x轴交于点A，如图，则B（0，-4），
在Rt△AOB中，∵tan∠ABO=tanα=

OA

OB

=

1

2

，
∴OA=

1

2

OB=2，
∴A点坐标为（2，0）或（-2，0），
把A（2，0）代入y=kx-4得2k-4=0，解得k=2；
把A（-2，0）代入y=kx-4得-2k-4=0，解得k=-2，
即k的值为2或-2．
故答案为2或-2．

点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了一次函数图象上点的坐标特征．