
【题目】下列结论:①若![]() ,则关于x的方程 ax-b+c=0(a
,则关于x的方程 ax-b+c=0(a![]() 的解是x=-1;②若x=1是方程ax+b+c=1且a
的解是x=-1;②若x=1是方程ax+b+c=1且a![]() 的解,则a+b+c=1成立;③若
的解,则a+b+c=1成立;③若![]() ,则
,则![]() ;④A、B、C是平面内的三个点,AB与AC是两条线段,若AB=AC,则点C为线段AB的中点;⑤若
;④A、B、C是平面内的三个点,AB与AC是两条线段,若AB=AC,则点C为线段AB的中点;⑤若![]() ,则
,则![]() 的值为0。其中正确结论的个数是( )
的值为0。其中正确结论的个数是( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
①求出b=2a,c=3a,然后代入方程求解即可;②根据方程解的定义代入即可;③根据题意可得a=-b,且a,b≠0,然后代入计算即可;④根据线段中点的定义判断即可;⑤首先求出z-y<0,x-z>0,y-x>0,然后利用绝对值的性质化简.
解:①∵![]() ,
,
∴b=2a,c=3a,
∴关于x的方程 ax-b+c=0可变形为:ax-2a+3a=0(a≠0),
解得:x=-1,故①正确;
②将x=1代入ax+b+c=1得:a+b+c=1,故②正确;
③∵![]() ,
,
∴a=-b,且a,b≠0,
∴![]() ,故③正确;
,故③正确;
④若A、B、C在同一条直线上,则点A为线段BC的中点,故④错误;
⑤∵![]() ,
,
∴z-y<0,x-z>0,y-x>0,
∴![]() ,故⑤正确,
,故⑤正确,
故选:C.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
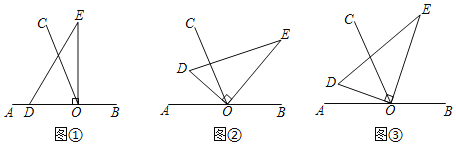
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
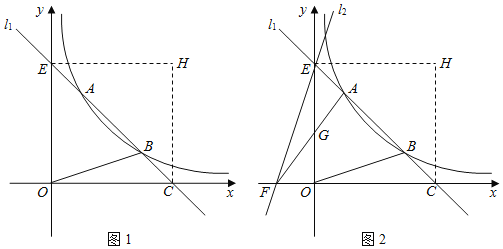
查看答案和解析>>
科目:初中数学 来源: 题型:
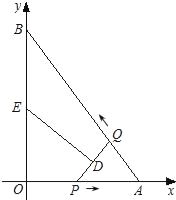
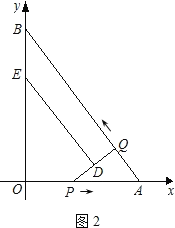
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
【答案】(1)直线AB的解析式为![]() ;(2)S=﹣
;(2)S=﹣![]() t2+
t2+![]() t;
t;
(3)四边形QBED能成为直角梯形.①t=![]() ;②当DE经过点O时,t=
;②当DE经过点O时,t=![]() 或
或![]() .
.
【解析】分析:(1)首先由在Rt△AOB中,OA=3,AB=5,求得OB的值,然后利用待定系数法即可求得一次函数的解析式;
(2)过点Q作QF⊥AO于点F.由△AQF∽△ABO,根据相似三角形的对应边成比例,借助于方程即可求得QF的长,然后即可求得![]() 的面积S与t之间的函数关系式;
的面积S与t之间的函数关系式;
(3)①分别从DE∥QB与PQ∥BO去分析,借助于相似三角形的性质,即可求得t的值;
②根据题意可知即![]() 时,则列方程即可求得t的值.
时,则列方程即可求得t的值.
详解:(1)在Rt△AOB中,OA=3,AB=5,由勾股定理得![]()
∴A(3,0),B(0,4).
设直线AB的解析式为y=kx+b.
∴![]() .解得
.解得
∴直线AB的解析式为![]()
(2)如图1,过点Q作QF⊥AO于点F.
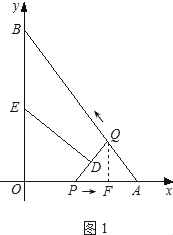
∵AQ=OP=t,∴AP=3t.
由△AQF∽△ABO,得![]()
∴![]()
∴![]()
∴![]()
∴![]()
(3)四边形QBED能成为直角梯形,
①如图2,当DE∥QB时,
∵DE⊥PQ,
∴PQ⊥QB,四边形QBED是直角梯形.
此时![]()
由△APQ∽△ABO,得![]()
∴![]()
解得![]()
如图3,当PQ∥BO时,
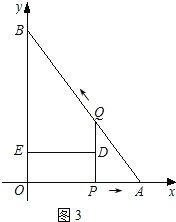
∵DE⊥PQ,
∴DE⊥BO,四边形QBED是直角梯形.
此时![]()
由△AQP∽△ABO,得![]()
即![]()
3t=5(3t),
3t=155t,
8t=15,
解得![]()
(当P从A向0运动的过程中还有两个,但不合题意舍去).
②当DE经过点O时,
∵DE垂直平分PQ,
∴EP=EQ=t,
由于P与Q相同的时间和速度,
∴AQ=EQ=EP=t,
∴∠AEQ=∠EAQ,
∵![]()
∴∠BEQ=∠EBQ,
∴BQ=EQ,
∴![]()
所以![]()
当P从A向O运动时,
过点Q作QF⊥OB于F,
EP=6t,
即EQ=EP=6t,
AQ=t,BQ=5t,
∴![]()
∴![]()
∵![]()
即![]()
解得:![]()
∴当DE经过点O时, ![]() 或
或![]() .
.
点睛:本题考查知识点较多,勾股定理,待定系数法求一次函数解析式,相似三角形的判定与性质等知识点,熟练掌握和运用各个知识点是解题的关键.
【题型】解答题
【结束】
21
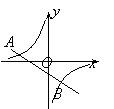
【题目】如图,反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)的图象相交于A、B两点,点A的坐标为(-6,2),点B的坐标为(3,n).求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
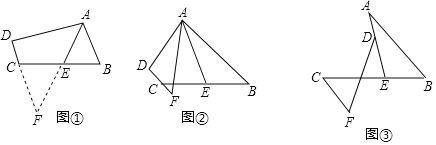
【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com