练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，中，，是的中点，的垂直平分线分别交于点，连接，则图中全等的三角形有（ ）

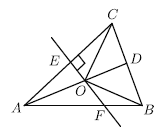
    A.1对B.2对C.3对D.4对

    【答案】D

    【解析】

    根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OC，然后判断出△AOE和△COE全等，再根据等腰三角形三线合一的性质可得AD⊥BC，从而得到△ABC关于直线AD轴对称，再根据全等三角形的定义写出全等三角形即可得解．

    解：∵EF是AC的垂直平分线，
    ∴OA=OC，
    又∵OE=OE，
    ∴Rt△AOE≌Rt△COE，
    ∵AB=AC，D是BC的中点，
    ∴AD⊥BC，
    ∴△ABC关于直线AD轴对称，
    ∴△AOC≌△AOB，△BOD≌△COD，△ABD≌△ACD，
    综上所述，全等三角形共有4对．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料：各类方程的解法

    求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．

    用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x3+x2-2x=0，可以通过因式分解把它转化为x(x2+x-2)=0，解方程x=0和x2+x-2=0，可得方程x3+x2-2x=0的解．

    （1）问题：方程x3+x2-2x=0的解是x1=0,x2= ，x3= ；

    （2）拓展：用“转化”思想求方程的解；

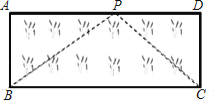
    （3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是BC边的中点，DE⊥BC交AB于点E，AD=AC，EC交AD于点F．

    (1)求证：△ABC∽△FCD；

    (2)求证：FC=3EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′OP=r2，则称点P′是点P关于⊙O的“反演点”．

    如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以等腰△ABC的腰AB为⊙O的直径交底边BC于D，DE⊥AC于E．

    求证：（1）DB＝DC；

    （2）DE为⊙O的切线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

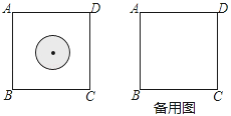
    【题目】有一类随机事件概率的计算方法：设试验结果落在某个区域S中的每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A）=． 有一块边长为30cm的正方形ABCD飞镖游戏板，假设飞镖投在游戏板上的每一点的机会均等．求下列事件发生的概率：

    (1)在飞镖游戏板上画有半径为5cm的一个圆（如图1），求飞镖落在圆内的概率；

    (2)飞镖在游戏板上的落点记为点O，求△OAB为钝角三角形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

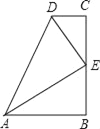
    【题目】在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有（　　）个．

    （1）AE平分∠DAB；（2）△EBA≌△DCE；（3）AB+CD=AD；（4）AE⊥DE；（5）AB∥CD．

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为节约水资源，从2018年1月1日起调整居民用水价格，每立方米水费比2017年上涨．小明家2017年8月的水费是18元，而2018年8月的水费是33元．已知小明家2018年8月的用水量比2017年8月的用水量多5 m3．

    （1）求该市2017年居民用水的价格；

    （2）小明家2019年8月用水量比2018年8月份用水量多了20%，求小明家2019年8月份的水费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

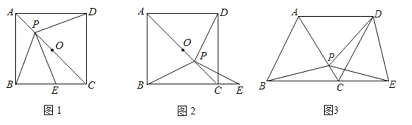
    【题目】如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE＝PB，连接PD，O为AC中点．

    （1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，请说明理由；

    （2）①如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由；

    ②如图2，试用等式来表示PB,BC,CE之间的数量关系，并证明．

    （3）如图3，把正方形ABCD改为菱形ABCD，其他条件不变，当时，连接DE，试探究线段PB与线段DE的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案