
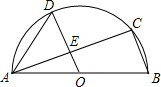
 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.分析 (1)由∠D=70°,可求得∠AOD的度数,由AB是半圆O的直径,根据直径所对的圆周角是直角,可求得∠C=90°,又由OD∥BC,证得OD⊥AC,然后由垂径定理求得$\widehat{AD}$=$\widehat{CD}$,再由圆周角定理求得∠CAD的度数;
(2)由垂径定理可求得AE的长,然后设OA=x,则OE=OD-DE=x-2,在Rt△OAE中,OE2+AE2=OA2,可得方程(x-2)2+42=x2,解此方程即可求得答案.
解答 解:(1)∵OA=OD,∠D=70°,
∴∠OAD=∠D=70°,
∴∠AOD=180°-∠OAD-∠D=40°,
∵AB是半圆O的直径,
∴∠C=90°,
∵OD∥BC,
∴∠AEO=∠C=90°,
即OD⊥AC,
∴$\widehat{AD}$=$\widehat{CD}$,
∴∠CAD=$\frac{1}{2}$∠AOD=20°;
(2)∵AC=8,OE⊥AC,
∴AE=$\frac{1}{2}$AC=4,
设OA=x,则OE=OD-DE=x-2,
∵在Rt△OAE中,OE2+AE2=OA2,
∴(x-2)2+42=x2,
解得:x=5,
∴OA=5,
∴AB=2OA=10.
点评 此题考查了圆周角定理、垂径定理以及勾股定理.注意得到OD⊥AC,应用垂径定理是关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 向左平移4个单位 | B. | 向右平移4个单位 | C. | 向上平移4个单位 | D. | 向下平移4个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
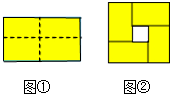 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )| A. | (m-n)2 | B. | (m+n)2 | C. | 2mn | D. | m2-n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 3,3 | B. | 3,3.5 | C. | 3.5,3.5 | D. | 3.5,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 878.97×108元 | B. | 878.97×109元 | C. | 8.7897×1010元 | D. | 8.7897×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com