
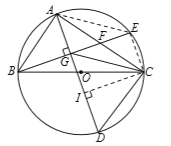
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,弦
上一点,弦![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() .
.
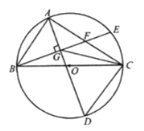
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)证法一:连接![]() ,利用圆周角定理得到
,利用圆周角定理得到![]() ,从而证明
,从而证明![]() ,然后利用同弧所对的圆周角相等及三角形外角的性质得到
,然后利用同弧所对的圆周角相等及三角形外角的性质得到![]() ,从而使问题得解;证法二:连接
,从而使问题得解;证法二:连接![]() ,
,![]() ,由圆周角定理得到
,由圆周角定理得到![]() ,从而判定
,从而判定![]() ,得到
,得到![]() ,然后利用圆内接四边形对角互补可得
,然后利用圆内接四边形对角互补可得![]() ,从而求得
,从而求得![]() ,使问题得解;
,使问题得解;
(2)首先利用勾股定理和三角形面积求得AG的长,解法一:过点![]() 作
作![]() 于点
于点![]() ,利用勾股定理求GH,CH,CD的长;解法二:过点
,利用勾股定理求GH,CH,CD的长;解法二:过点![]() 作
作![]() 于点
于点![]() ,利用AA定理判定
,利用AA定理判定![]() ,然后根据相似三角形的性质列比例式求解.
,然后根据相似三角形的性质列比例式求解.
(1)证法一:连接![]() .
.
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,
,
∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∴![]() .
.
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() .
.
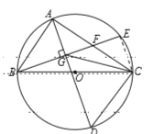
证法二:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,∴
的直径,∴![]()
∵![]()
∴![]()
∴![]() ,
,
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵四边形![]() 内接于
内接于![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]() .
.
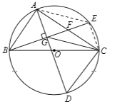
(2)解:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
根据勾股定理得![]() .
.
连接![]() ,
,![]()
∵![]() 为
为![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() .
.
在![]() 中,
中,![]()
![]() ,
,
∴![]()
解法一:过点![]() 作
作![]() 于点
于点![]()
∴![]()
在![]() 中,
中,![]() ,
,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
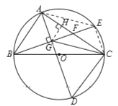
解法二:过点![]() 作
作![]() 于点
于点![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴四边形![]() 为矩形
为矩形
∴![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]()
∴![]() .
.
∵![]() ,
,![]()
∴![]()
∴![]() 即
即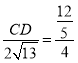
∴![]()


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
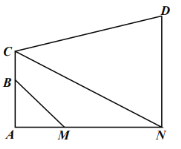
【题目】如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,S是矩形ABCD的AD边上一点,点E以每秒kcm的速度沿折线BS-SD-DC匀速运动,同时点F从点C出发点,以每秒1cm的速度沿边CB匀速运动.已知点F运动到点B时,点E也恰好运动到点C,此时动点E,F同时停止运动.设点E,F出发t秒时,△EBF的面积为![]() .已知y与t的函数图像如图2所示.其中曲线OM,NP为两段抛物线,MN为线段.则下列说法:
.已知y与t的函数图像如图2所示.其中曲线OM,NP为两段抛物线,MN为线段.则下列说法:
①点E运动到点S时,用了2.5秒,运动到点D时共用了4秒;
②矩形ABCD的两邻边长为BC=6cm,CD=4cm;
③sin∠ABS=![]() ;
;
④点E的运动速度为每秒2cm.其中正确的是( )
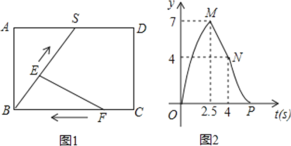
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.如图,在平面直角坐标系xOy中,已知抛物线y=x2﹣2x,其顶点为A.
(1)试求抛物线y=x2﹣2x的“不动点”的坐标;
(2)平移抛物线y=x2﹣2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线的表达式.
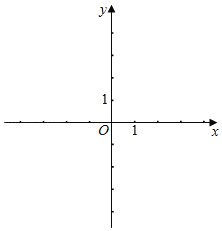
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永农化工厂以每吨800元的价格购进一批化工原料,加工成化工产品进行销售,已知每1吨化工原料可以加工成化工产品0.8吨,该厂预计销售化工产品不超过50吨时每吨售价为1600元,超过50吨时,每超过1吨产品,销售所有的化工产品每吨价格均会降低4元,设该化工厂生产并销售了x吨化工产品.
(1)用x的代数式表示该厂购进化工原料 吨;
(2)当x>50时,设该厂销售完化工产品的总利润为y,求y关于x的函数关系式;
(3)如果要求总利润不低于38400元,那么该厂购进化工原料的吨数应该控制在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨举办首届《诗词大会》,九年级2班的马小梅晋级总决赛,比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:横扫千军、你说我猜、初级飞花令,(分别用![]() )表示;
)表示;
第二环节:出口成诗、飞花令、超级飞花令、诗词接龙(分别用![]() 表示).
表示).
(1)请用画树状图或列表的方法表示马小梅参加总决赛抽取题目的所有可能结果;
(2)求马小梅参加总决赛抽取题目都是飞花令题目(初级飞花令、飞花令、超级飞花令)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月27日,我国成功发射了“长征五号”遥三运载火箭.如图,“长征五号”运载火箭从地面![]() 处垂直向上发射,当火箭到达
处垂直向上发射,当火箭到达![]() 处时,从位于地面
处时,从位于地面![]() 处的雷达站测得此时仰角
处的雷达站测得此时仰角![]() ,当火箭继续升空到达
,当火箭继续升空到达![]() 处时,从位于地面
处时,从位于地面![]() 处的雷达站测得此时仰角
处的雷达站测得此时仰角![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)若“长征五号”运载火箭在![]() 处进行“程序转弯”,且
处进行“程序转弯”,且![]() ,求雷达站
,求雷达站![]() 到其正上方点
到其正上方点![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先锋中学数学课题组为了了解初中学生阅读数学教科书的现状,随机抽取某校部分初中学生进行调查,调查结果分为“重视”、“一般”、“不重视”、“说不清楚”四种情况(依次用A、B、C、D表示),依据相关数据绘制成以下不完整的统计表和统计图,请根据图表中的信息解答下列问题:
类别 | 频数 | 频率 |
重视 | a | 0.25 |
一般 | 60 | 0.3 |
不重视 | b | c |
说不清楚 | 10 | 0.05 |
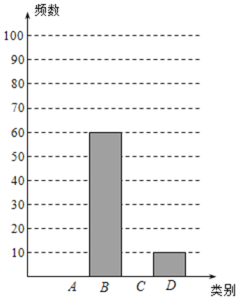
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有2000名学生,请估计该校“不重视阅读数学教科书”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com