
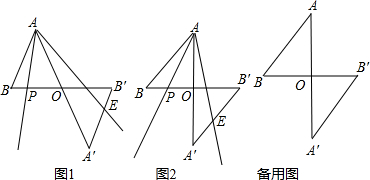
���� ��1���ɵȱ������ε����ʵõ�AA��=2AB�����ɵȱ������κ���ת�������жϳ���ABP�ס�AA��E�����ɣ�
��2���ɵ���ֱ�������ε����ʵõ�AA��=2AB�����ɵ���ֱ�������κ���ת�������жϳ���ABP�ס�AA��E�����ɣ�
��3���ɣ�2���Ľ��۽��ͼ�εõ�B��E=$\sqrt{2}$��2-BP����B��P=BB��-BP=4-BP�������������ε�����������̣����BP��B��M������ù��ɶ������㼴�ɣ�
��� �⣺��1���ߡ�A��OB���ǡ�AOB��ת�õ���
���B=��A�䣬AB=OA��=A��B�䣬
��AA��=2AB��
����ת�ã���BAP=��A��AE��
���ABP�ס�AA��E��
��$\frac{BP}{A��E}$=$\frac{AB}{AA��}$=$\frac{1}{2}$��
��2BP=A��E��
��A��E=A��B��-B��E=AB-B��E��
��2BP=AB-B��E��
��2BP+B��E=AB��
��2���ڡ�AOB�У�OA=OB����AOB=90�㣬
���AOBΪ����ֱ�������Σ�
�ߡ�AOB��ת�õ���A��OB�䣬
��A��B��=AB=$\sqrt{2}$OA=$\sqrt{2}$OA�䣬AA��=2OA����B=��A��=45�㣬
�ߡ�BAO=��PAE=45�㣬
���BAP=��A��AE��
�ߡ�B=��A�䣬
���BAP���ס�A��AE��
��$\frac{BP}{A��E}=\frac{AB}{A��A}=\frac{\sqrt{2}OA}{2OA}=\frac{1}{\sqrt{2}}$��
��$\sqrt{2}$BP=A��E=A��B��-B��E=AB-B��E��
��$\sqrt{2}$BP+B��E=AB��
��3����ͼ��
����E��EF��BB�䣬����M��MG��BB�䣬
�ߡ�A��B��B=45�㣬
��EF=B��Esin��A��B��B=$\frac{1}{\sqrt{2}}$B��E=$\frac{1}{\sqrt{2}}$��AB-$\sqrt{2}$BP��=$\frac{1}{\sqrt{2}}$��2$\sqrt{2}$-$\sqrt{2}$BP��=2-BP��
�ɣ�2���У�$\sqrt{2}$BP+B��E=AB��
��B��E=AB-$\sqrt{2}$BP��
��AB=2$\sqrt{2}$��
��B��E=2$\sqrt{2}$-$\sqrt{2}$BP=$\sqrt{2}$��2-BP����
��BB��=2OB=4��
��B��P=BB��-BP=4-BP��
��S=$\frac{1}{2}$B��P��EF=$\frac{1}{2}$��4-BP����2-BP��=$\frac{3}{2}$��
�ࣨ4-BP����2-BP��=3��
��BP=1��BP=5���ᣩ��
��BP=1��
��PF=2��B��P=3��B��E=$\sqrt{2}$��
��EF��BB�䣬MG��BB�䣬
��EF��MG��
��$\frac{PF}{B��P+B��G}=\frac{EF}{GM}$��
��B��G=GM��
��$\frac{2}{5+GM}=\frac{1}{GM}$
��GM=3��
��B��G=3��
��B��M=3$\sqrt{2}$��
��B��E=$\sqrt{2}$��
��EM=$\sqrt{B��{E}^{2}+B��{M}^{2}}$=2$\sqrt{5}$��
���� �����Ǽ��α任�ۺ��⣬��Ҫ��������ת���ȱ������ε����ʣ�����ֱ�������ε����ʣ����������ε��ж������ʣ�������������GM���ǽⱾ��Ĺؼ���Ҳ���ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=$\frac{1}{2}{x}^{2}$+��m-2��x+2m-6�ĶԳ���Ϊֱ��x=1����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��֪������y=$\frac{1}{2}{x}^{2}$+��m-2��x+2m-6�ĶԳ���Ϊֱ��x=1����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
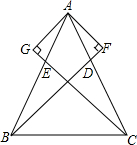 ��֪����ͼ���ڡ�ABC�У�AB=AC��BD��CE�ֱ�ΪAC��AB���ϵ����ߣ�AF��BD��F��AG��CE��G����֤��AF=AG��
��֪����ͼ���ڡ�ABC�У�AB=AC��BD��CE�ֱ�ΪAC��AB���ϵ����ߣ�AF��BD��F��AG��CE��G����֤��AF=AG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
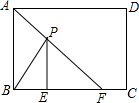 ��ͼ���ھ���ABCD�У�AB=4cm��AD=5cm����E��BC���ϣ���BE=1cm��AFƽ�֡�BAD��ͼ��PΪAF������һ�㣬��PΪAF������һ���㣬��ȷ��һ��P������BP��EP����BP+EP����СֵΪ5cm��
��ͼ���ھ���ABCD�У�AB=4cm��AD=5cm����E��BC���ϣ���BE=1cm��AFƽ�֡�BAD��ͼ��PΪAF������һ�㣬��PΪAF������һ���㣬��ȷ��һ��P������BP��EP����BP+EP����СֵΪ5cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com