练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，把一个转盘分成四等份，依次标上数字1、2、3、4，若连续自由转动转盘二次，指针指向的数字分别记作把作为点的横、纵坐标．

    【1】求点A（a，b）的个数；

    【2】求点A（a，b）在函数的图象上的概率．

    【答案】

    【1】 列表或画树状图



    1

    2

    3

    4

    1

    （1，1）

    （2，1）

    （3，1）

    （4，1）

    2

    （1，2）

    （2，2）

    （3，2）

    （4，2）

    3

    （1，3）

    （2，3）

    （3，3）

    （4，3）

    4

    （1，4）

    （2，4）

    （3，4）

    （4，4）

    因此，点的个数共有16个； （3分）

    【2】 由（1）得，可能出现的结果有16种，它们出现的可能性是相同的．若点在上，则，由（1）得，因此，点在函数图象上的概率为．

    【解析】

    依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．

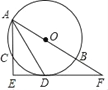
    （1）求证：EF是⊙O的切线；

    （2）若AC=4，CE=2，求的长度．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2＝(1＋)2.善于思考的小明进行了以下探索：设a＋b＝(m＋n)2(其中a，b，m，n均为整数)，则有a＋b＝m2＋2n2＋2mn，∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把类似a＋b的式子化为平方式的方法．请你仿照小明的方法解决下列问题：

    (1)当a，b，m，n均为正整数时，若a＋b＝(m＋n)2，用含m，n的式子分别表示a，b，得a＝______________，b＝________；

    (2)利用所探索的结论，找一组正整数a，b，m，n填空：

    ________＋________＝(________＋________)2；

    (3)若a＋4＝(m＋n)2，且a，m，n均为正整数，求a的值．

    (4)试化简.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：若m2﹣2mn+2n2﹣10n+25＝0，求m，n的值．

    解：∵m2﹣2mn+2n2﹣10n+25＝0，

    ∴（m2﹣2mn+n2）+（n2﹣10n+25）＝0．

    ∴（m﹣n）2+（n﹣5）2＝0，

    ∴m﹣n＝0，n﹣5＝0．

    ∴n＝5，m＝5．

    根据你的观察，探究下面的问题：

    （1）已知：x2+2xy+2y2+4y+4＝0，求xy的值；

    （2）已知：△ABC的三边长a，b，c都是正整数，且满足：a2+b2﹣16a﹣12b+100＝0，求△ABC的周长的最大值；

    （3）已知：△ABC的三边长是a，b，c，且满足：a2+2b2+c2﹣2b（a+c）＝0，试判断△ABC是什么形状的三角形并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着智能手机的普及，微信抢红包已成为春节期间人们最喜欢的活动之一，某校七年级（1）班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．请根据以上信息回答：

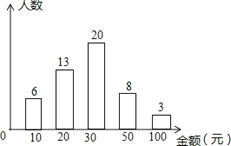
    （1）该班同学所抢红包金额的众数是______，

    中位数是______；

    （2）该班同学所抢红包的平均金额是多少元？

    （3）若该校共有18个班级，平均每班50人，请你估计该校学生春节期间所抢的红包总金额为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，则△CEF的面积最大值是____．

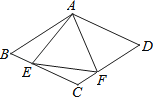
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，，点是的中点，平分，.

    （1）求证：；

    （2）若，试判断的形状，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC是以AB为直径的⊙O的弦，点D是⊙O上的一点，过点D作⊙O的切线交直线AC于点E，AD平分∠BAE，若AB＝10，DE＝3，则AE的长为____________．

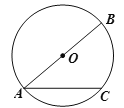
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：分别与x轴、y轴交于点B、C，且与直线l2：交于点A．

    （1）求出点A的坐标

    （2）若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式

    （3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案