
【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
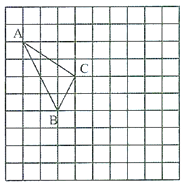
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请把△ABC先向右移动5个单位,再向下平移3个单位得到△![]() ,在图中画出△
,在图中画出△![]() ;
;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
(2)如表是y与x的几组对应值
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m等于多少;
②若A(n,2018),B(2020,2018)为该函数图象上不同的两点,则n等于多少;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并根据描出的点画出该函数的图象;根据函数图象可得:该函数的最小值为多少;该函数图象与x轴围成的几何图形的面积等于多少;
(4)已知直线y1=![]() x﹣
x﹣![]() 与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.
与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图中C型黑白一样)按某种规律组成的一个大正方形。现有25×25格式的正方形如图,角上是三个7×7的A型大黑白相间正方形,中间右下有一个5×5的B型黑白相间正方形((A,B型均由C型黑白两色小正方形组成),除这4个正方形外,其他的C型小正方形黑色块数正好是白色块数的3倍多53块,则该25×25格式的二维码中除去A、B型后,有__块C型白色小正方形,整个二维码中共有__块C型白色小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
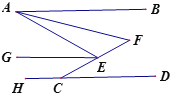
【题目】如图,已知AB∥HD,EG平分∠AEC,EG∥AB,AF平分∠BAE,CE的延长线交AF于点F,若∠HCE=![]() °,∠F=
°,∠F=![]() °,用含
°,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() =_______
=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一矩形纸片OABC放入平面直角坐标系xoy中,使OA,OC分别落在x轴、y轴上,现将纸片OABC沿OB折叠,折叠后点A落在点A'的位置,若OA=1,OB=2,则点A'的坐标为( )
A.![]()
B.![]()
C.( ![]() )
)
D.( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com