
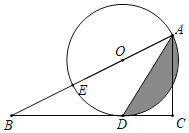
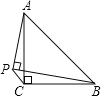
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.
(1)求证:直线BC是⊙O的切线;
(2)若∠B=30°,AC=3,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() π-
π-![]() .
.
【解析】
(1)连接OD,由AD平分∠BAC,可知∠OAD=∠CAD,易证∠ODA=∠OAD,所以∠ODA=∠CAD,所以OD∥AD,由于∠C=90°,所以∠ODB=90°,从而可证直线BC是⊙O的切线;
(2)根据含30度角的直角三角形性质可求出AB的长度,然后求出∠AOD的度数,然后根据扇形的面积公式即可求出答案.
解:(1)连接OD,
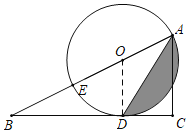
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AD,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴直线BC是⊙O的切线;
(2)由∠B=30°,∠C=90°,∠ODB=90°,
得:AB=2AC=6,OB=2OD,∠AOD=120°,
∠DAC=30°,
∵OA=OD,
∴OB=2OA,
∴OA=OD=2,
由∠DAC=30°,得DC=![]() ,
,
∴S阴影=S扇形OAD-S△OAD
=![]() π×4-
π×4-![]() ×2×
×2×![]()
=![]() π-
π-![]() .
.


科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
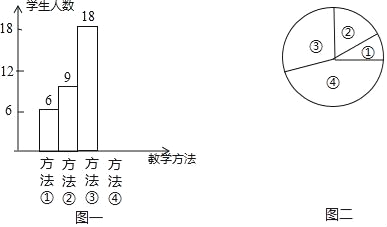
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2与点D.已知l1与l2的距离为1,l2与l3的距离为3,则线段CD的长等于______.
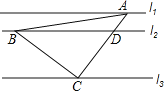
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=![]() ,以AB为斜边另作Rt△APB,连接PC,当点P在AC左侧时,下列结论正确的是( )
,以AB为斜边另作Rt△APB,连接PC,当点P在AC左侧时,下列结论正确的是( )
A. ![]() 的度数不确定B.
的度数不确定B. ![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
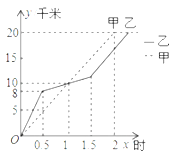
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
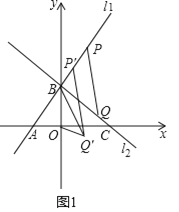
【题目】如图,直线l1:y=![]() x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
(1)求直线l2的解析式,并直接判断△ABC的形状(不需说明理由);
(2)如图1,P为直线l1上一点,横坐标为12,Q为直线l2上一动点,当PQ+![]() CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极绘就我市“一福地、四名城”建设的宏伟蓝图,某镇大力发展旅游业,一店铺专门售卖地方特产“曲山老鹅”,以往销售数据表明,该“曲山老鹅”每天销售数量y(只)与销售单价x(元)满足一次函数y=-![]() x+110,每只“曲山老鹅”各项成本合计为20元/只.
x+110,每只“曲山老鹅”各项成本合计为20元/只.
(1)该店铺“曲山老鹅”销售单价x定为多少时,每天获利最大?最大利润是多少?
(2)该店店主关心教育,决定今后的一段时间从每天的销售利润中捐出200元给当地学校作为本学期优秀学生的奖励资金,为了保证该店捐款后每天剩余利润不低于4000元,试确定该“曲山老鹅”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com