
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣![]() x+4上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,根据图形所反映的规律,S2019=( )
x+4上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,根据图形所反映的规律,S2019=( )
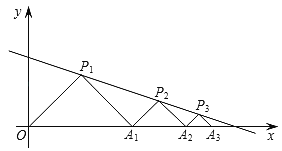
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
分别过点P1、P2、P3作x轴的垂线段,先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高,继而求得三角形的面积,得出面积的规律即可得出答案.
解:如图,分别过点P1、P2、P3作x轴的垂线段,垂足分别为点C、D、E,
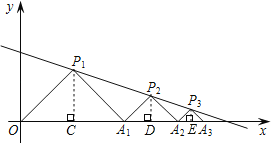
∵P1(3,3),且△P1OA1是等腰直角三角形,
∴OC=CA1=P1C=3,
设A1D=a,则P2D=a,
∴OD=6+a,
∴点P2坐标为(6+a,a),
将点P2坐标代入y=﹣![]() x+4,得:﹣
x+4,得:﹣![]() (6+a)+4=a,
(6+a)+4=a,
解得:a=![]() ,
,
∴A1A2=2a=3,P2D=![]() ,
,
同理求得P3E=![]() 、A2A3=
、A2A3=![]() ,
,
∵S1=![]() ×6×3=9×(
×6×3=9×(![]() )0、S2=
)0、S2=![]() ×3×
×3×![]() =9×(
=9×(![]() )、
)、
S3=![]() ×
×![]() ×
×![]() =9×(
=9×(![]() )2、……
)2、……
∴S2019=9×(![]() )2018.
)2018.
故选:A.


科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球,篮球,乒乓球,排球,足球五项球类运动,每位同学必须且只能选择一项运动项目.对全校学生选取![]() 进行随机抽样调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行随机抽样调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 |
|
篮 球 |
|
乒乓球 |
|
排 球 |
|
足 球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() = ,
= ,![]() = .
= .
(2)在扇形统计图中,“羽毛球”所在的扇形的圆心角的度数为 ;
(3)全校有多少名学生选择参加篮球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
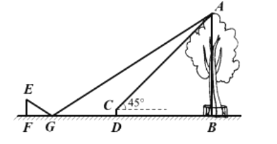
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装着分别标有数字![]() ,
,![]() ,0,2的四个小球,除数字不同外,小球没有任何区别,每次实验时把小球搅匀.
,0,2的四个小球,除数字不同外,小球没有任何区别,每次实验时把小球搅匀.
(1)从中任取一球,求所抽取的数字恰好为负数的概率;
(2)从中任取一球,将球上的数字记为![]() ,然后把小球放回;再任取一球,将球上的数字记为
,然后把小球放回;再任取一球,将球上的数字记为![]() ,试用画树状图(或列表法)表示出点
,试用画树状图(或列表法)表示出点![]() 所有可能的结果,并求点
所有可能的结果,并求点![]() 在直线
在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
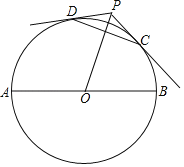
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
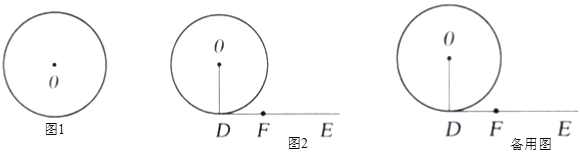
【题目】(1)①如图1,请用直尺(不带刻度)和圆规作出![]() 的内接正三角形
的内接正三角形![]() (按要求作图,不要求写作法,但要保留作图痕迹).
(按要求作图,不要求写作法,但要保留作图痕迹).
②若![]() 的内接正三角形
的内接正三角形![]() 边长为6,求
边长为6,求![]() 的半径;
的半径;
(2)如图2,![]() 的半径就是(1)中所求半径的值.点
的半径就是(1)中所求半径的值.点![]() 在
在![]() 上,
上,![]() 是
是![]() 的切线,点
的切线,点![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,点
方向移动,点![]() 是
是![]() 上的点(不与点
上的点(不与点![]() 重合),
重合),![]() 是
是![]() 的切线.设点
的切线.设点![]() 运动的时间为
运动的时间为![]() (秒),当
(秒),当![]() 为何值时,
为何值时,![]() 是直角三角形,请你求出满足条件的所有
是直角三角形,请你求出满足条件的所有![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com