
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD= ![]() ,求AD的长.
,求AD的长.
【答案】
(1)证明:∵ AD⊥BC,∠BAD=45°,
∴ ∠ABD=∠BAD=45°.
∴ AD=BD.
∵ AD⊥BC,BE⊥AC,
∴ ∠CAD+∠ACD=90°,∠CBE+∠ACD=90o
∴ ∠CAD=∠CBE.
又∵ ∠CDA=∠FDB=90°,
∴ △ADC≌△BDF.
∴ AC=BF.
∵ AB=BC,BE⊥AC,
∴ AE=EC,即AC=2AE.
∴ BF=2AE
(2)解:∵ △ADC≌△BDF,∴ DF=CD= ![]() .
.
∴ 在Rt△CDF中,CF= ![]() =2.
=2.
∵ BE⊥AC,AE=EC,∴ AF=FC=2.
∴ AD=AF+DF=2+ ![]()
【解析】(1)由AD⊥BC,∠BAD=45°,证得AD=BD.再根据垂直的定义及同角的余角相等得出∠CAD=∠CBE.因此证明△ADC≌△BDF,得出AC=BF.即可得出结论。
(2)由△ADC≌△BDF得出DF=CD,在Rt△CDF中,利用勾股定理求出CF的长,从而求出AD的长。


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】为提高全民健康意识,2018年11月25日共青团宝应县委继续组织了一次万人参加的“全民健康行”毅行活动,这次毅行活动的行程约为20000m,将20000m用科学记数法表示为______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线![]() :y=x﹣1
:y=x﹣1
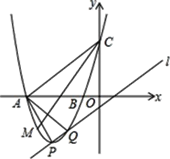
(1)求证:点P在直线![]() 上;
上;
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线![]() 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线![]() 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)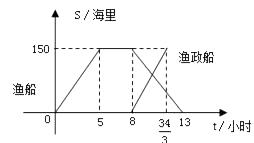
(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一个点从A(a1 , a2)出发沿图中路线依次经过B(a3 , a4),C(a5 , a6),D(a7 , a8),…,按此一直运动下去,则a2015+a2016的值为 . 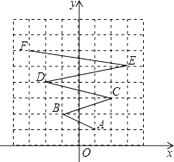
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国倡导的“一带一路”建设将促进我国与世界各国的互利合作,“一带一路”地区覆盖总人口约为4400000000人,将数据4400000000用科学记数法表示为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com