
【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线![]() :y=x﹣1
:y=x﹣1
(1)求证:点P在直线![]() 上;
上;
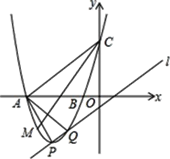
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线![]() 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线![]() 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
【答案】(1)证明见解析;(2)(﹣4,﹣3);(3)m的值为0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
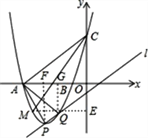
【解析】分析:(1)利用配方法得到y=(x-m)+m-1,点P(m,m-1),然后根据一次函数图象上点的坐标特征判断点P在直线l上;(2)当m= -3时,抛物线解析式为y=x+6x+5,根据抛物线与x轴的交点问题求出A(-5,0),易得C(0,5),通过解方程组![]() 得P(-3,-4),Q(-2,-3),作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,证明Rt△CME∽Rt△PAF,利用相似得
得P(-3,-4),Q(-2,-3),作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,证明Rt△CME∽Rt△PAF,利用相似得![]() ,设M(x,x+6x+5),则
,设M(x,x+6x+5),则![]() ,解得
,解得![]() =0(舍去),
=0(舍去),![]() = -4,于是得到点M的坐标为(-4,-3);(3)通过解方程组
= -4,于是得到点M的坐标为(-4,-3);(3)通过解方程组
![]() 得P(m,m-1),Q(m+1,m),利用两点间的距离公式得到PQ=2,OQ=2m+2m+1,OP=2m-2m+1,然后分类讨论:当PQ=OQ时,2m+2m+1=2;当PQ=OP时,2m-2m+1=2;当OP=OQ时,2m+2m+1=2m-2m+1,再分别解关于m的方程求出m即可.
得P(m,m-1),Q(m+1,m),利用两点间的距离公式得到PQ=2,OQ=2m+2m+1,OP=2m-2m+1,然后分类讨论:当PQ=OQ时,2m+2m+1=2;当PQ=OP时,2m-2m+1=2;当OP=OQ时,2m+2m+1=2m-2m+1,再分别解关于m的方程求出m即可.
本题解析:
(1)证明:∵y=x2﹣2mx+m2+m﹣1=(x﹣m)2+m﹣1,
∴点P的坐标为(m,m﹣1),
∵当x=m时,y=x﹣1=m﹣1,
∴点P在直线l上;
(2)解:当m=﹣3时,抛物线解析式为y=x2+6x+5,
当y=0时,x2+6x+5=0,解得x1=﹣1,x2=﹣5,则A(﹣5,0),
当x=0时,y=x2+6x+5=5,则C(0,5),
可得解方程组![]() ,解得
,解得![]() 或
或![]() ,
,
则P(﹣3,﹣4),Q(﹣2,﹣3),
作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,
∵OA=OC=5,
∴△OAC为等腰直角三角形,
∴∠ACO=45°,
∴∠MCE=45°﹣∠ACM,
∵QG=3,OG=2,
∴AG=OA﹣OG=3=QG,
∴△AQG为等腰直角三角形,
∴∠QAG=45°,
∵∠APF=90°﹣∠PAF=90°﹣(∠PAQ+45°)=45°﹣∠PAQ,
∵∠ACM=∠PAQ,
∴∠APF=∠MCE,
∴Rt△CME∽Rt△PAF,
∴![]() ,
,
设M(x,x2+6x+5),
∴ME=﹣x,CE=5﹣(x2+6x+5)=﹣x2﹣6x,
∴![]() ,
,
整理得x2+4x=0,解得x1=0(舍去),x2=﹣4,
∴点M的坐标为(﹣4,﹣3);
(3)解:解方程组![]() 得
得![]() 或
或![]() ,则P(m,m﹣1),Q(m+1,m),
,则P(m,m﹣1),Q(m+1,m),
∴PQ2=(m+1﹣m)2+(m﹣m+1)2=2,OQ2=(m+1)2+m2=2m2+2m+1,OP2=m2+(m﹣1)2=2m2﹣2m+1,
当PQ=OQ时,2m2+2m+1=2,解得m1=![]() ,m2=
,m2=![]() ;
;
当PQ=OP时,2m2﹣2m+1=2,解得m1=![]() ,m2=
,m2=![]() ;
;
当OP=OQ时,2m2+2m+1=2m2﹣2m+1,解得m=0,
综上所述,m的值为0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,设每千克应涨价x元,则可列方程为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线 ![]() 成轴对称的△A
成轴对称的△A ![]() ;
;
(2)线段 ![]() 被直线
被直线 ![]() ;
;
(3)在直线 ![]() 上找一点P,使PB+PC的长最短,并算出这个最短长度.
上找一点P,使PB+PC的长最短,并算出这个最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
(2)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
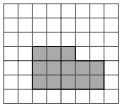
【题目】如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形.请在如图所示的网格中(网格的边长为1)中,用直尺作出这个大正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
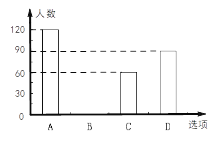
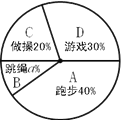
请结合统计图,回答下列问题:
(1)本次调查学生共 人, ![]() = ,并将条形图补充完整;
= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.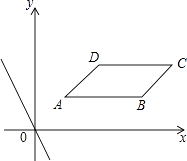
(1)k=;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com