

���� ��1������ͼ2��ʾ���������ε�������ʿɵá�EMC=��FMB=��DFE-��ABC��
��2������ͼ3��ʾ����Rt��ACF�У���ֱ�������μ��ɵó�FC�ij���
��3������������ǰ���˶����̣���ȷ��ͬʱ���ص�ͼ�εı仯�������I����0��x��2ʱ�����ͼ1��ʾ����II����2��x��6-2$\sqrt{3}$ʱ�����ͼ2��ʾ����III����6-2$\sqrt{3}$��x��6ʱ�����ͼ3��ʾ��
���  �⣺��1������ͼ2��ʾ���������ǰ�DEF�У���FDE=90�㣬DF=4��DE=4$\sqrt{3}$��
�⣺��1������ͼ2��ʾ���������ǰ�DEF�У���FDE=90�㣬DF=4��DE=4$\sqrt{3}$��
��tan��DFE=$\frac{DE}{DF}$=$\sqrt{3}$��
���DFE=60�㣬
���EMC=��FMB=��DFE-��ABC=60��-45��=15�㣻
�ʴ�Ϊ��15�㣻
��2������ͼ3��ʾ����EF������Cʱ��
FC=$\frac{AC}{sin��AFC}$=$\frac{6}{sin60��}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$��
��3�������ǰ�DEF�˶������У�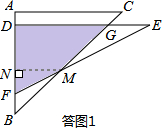
��I����0��x��2ʱ�����ͼ1��ʾ����DE��BC�ڵ�G��
����M��MN��AB�ڵ�N�����MNBΪ����ֱ�������Σ�MN=BN��
�֡�NF=$\frac{MN}{tan60��}$=$\frac{\sqrt{3}}{3}$MN��BN=NF+BF��
��NF+BF=MN����$\frac{\sqrt{3}}{3}$MN+x=MN��
��ã�MN=$\frac{3+\sqrt{3}}{2}x$��
y=S��BDG-S��BFM
=$\frac{1}{2}$BD•DG-$\frac{1}{2}$BF•MN
=$\frac{1}{2}$��x+4��2-$\frac{1}{2}$x•$\frac{3+\sqrt{3}}{2}$x
=-$\frac{\sqrt{3}+1}{4}$x2+4x+8��
��II����2��x��6-2$\sqrt{3}$ʱ�����ͼ2��ʾ��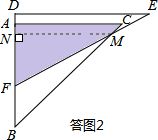 ����M��MN��AB�ڵ�N�����MNBΪ����ֱ�������Σ�MN=BN��
����M��MN��AB�ڵ�N�����MNBΪ����ֱ�������Σ�MN=BN��
�֡�NF=$\frac{MN}{tan60��}$=$\frac{\sqrt{3}}{3}$MN��BN=NF+BF��
��NF+BF=MN����$\frac{\sqrt{3}}{3}$MN+x=MN��
��ã�MN=$\frac{3+\sqrt{3}}{2}$x��
y=S��ABC-S��BFM
=$\frac{1}{2}$AB•AC-$\frac{1}{2}$BF•MN
=$\frac{1}{2}$��62-$\frac{1}{2}$x•$\frac{3+\sqrt{3}}{2}$x
=-$\frac{3+\sqrt{3}}{4}$x2+18��
��III����6-2$\sqrt{3}$��x��6ʱ�����ͼ3��ʾ����BF=x����AF=AB-BF=6-x��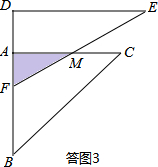
��AC��EF���ڵ�M����AM=AF•tan60��=$\sqrt{3}$��6-x����
y=S��AFM=$\frac{1}{2}$AF•AM=$\frac{1}{2}$��6-x��•$\sqrt{3}$��6-x��=$\frac{\sqrt{3}}{2}$x2-6$\sqrt{3}$x+18$\sqrt{3}$��
����������y��x�ĺ�������ʽΪ��
y=$\left\{\begin{array}{l}{-\frac{\sqrt{3}+1}{4}{x}^{2}+4x+8��0��x��2��}\\{-\frac{3+\sqrt{3}}{4}{x}^{2}+18��2��x��6-2\sqrt{3}��}\\{\frac{\sqrt{3}}{2}{x}^{2}-6\sqrt{3}x+18��6-2\sqrt{3}��x��6��}\end{array}\right.$��
���� ���������������ۺ��⣬����Ĺؼ�������������ǰ���˶����̣���ȷ��ͬʱ���ص�ͼ����״�ı仯������ڽ����������У����������Ǻ������м����⣬Ҳ�����������������ƣ���;ͬ�飮����ʱע���������˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڱ߳�Ϊ1��С��������ɵ������������н�����ͼ��ʾ��ƽ��ֱ������ϵ����֪���������ABC�������ε��������㶼��С�����εĶ����ϣ���
�ڱ߳�Ϊ1��С��������ɵ������������н�����ͼ��ʾ��ƽ��ֱ������ϵ����֪���������ABC�������ε��������㶼��С�����εĶ����ϣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�������屻��ȥһ��ֱ�������õ��ļ����壬�뻭���ü����������ͼ��
��ͼ��һ�������屻��ȥһ��ֱ�������õ��ļ����壬�뻭���ü����������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��2�� | B�� | ��-2��-1�� | C�� | ��2��-1�� | D�� | ��2��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com