
分析 (1)直接利用零指数幂的性质和立方根以及算术平方根的定义分别化简求出答案;
(2)直接利用绝对值的性质化简求出答案;
(3)直接利用平方根的定义分析得出答案;
(4)直接利用立方根的定义分析得出答案.
解答 解:(1)($\sqrt{3}$)2+$\sqrt{16}$-(π-3.14)0+$\root{3}{-8}$
=3+4-1-2
=4;
(2)|1-$\sqrt{2}$|+|$\sqrt{2}$-π|+|4-π|
=$\sqrt{2}$-1+π-$\sqrt{2}$+4-π
=3;
(3)(x-1)2-1=8
(x-1)2=9,
解得:x=4 或x=-2;
(4)(x+4)3=-64
则x+4=-4,
解得:x=-8.
点评 此题主要考查了实数运算以及立方根和平方根的定义,正确掌握相关运算法则是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
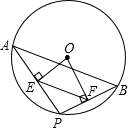 如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=8.
如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com