
分析 (1)公式法求解可得;
(2)因式分解法求解可得;
(2)整理成一般式后,因式分解法求解可得.
解答 解:(1)∵a=1,b=-2,c=-2,
∴△=4-4×1×(-2)=12>0,
则x=$\frac{2±2\sqrt{3}}{2}$=1$±\sqrt{3}$;
(2)∵(x-3)(x-3+4x)=0,即(x-3)(5x-3)=0,
∴x-3=0或5x-3=0,
解得:x=3或x=$\frac{3}{5}$;
(3)整理成一般式为x2+x-20=0,
∵(x-4)(x+5)=0,
∴x-4=0或x+5=0,
解得:x=4或x=-5.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
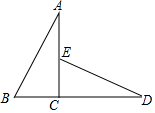 如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.
如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com