
分析 (1)把题目中所给数值相加,若结果为正数则B地在A地的东方,若结果为负数,则B地在A地的西方;
(2)分别计算出各点离出发点的距离,取数值较大的点即可;
(3)先求出这一天走的总路程,再计算出一共所需油量,减去油箱容量即可求出途中还需补充的油量.
解答 解:(1)∵14-9+8-7+13-6+10-5=18>0,
∴B地在A地的东边18千米;
(2)∵路程记录中各点离出发点的距离分别为:
14千米;14-9=5千米;
14-9+8=13千米;
14-9+8-7=6千米;
14-9+8-7+13=19千米;
14-9+8-7+13-6=13千米;
14-9+8-7+13-6+10=23千米;
14-9+8-7+13-6+10-5=18千米.
∴最远处离出发点23千米;
(3)∵这一天走的总路程为:14+|-9|+8+|-7|+13+|-6|+10+|-5|=72千米,
应耗油72×0.5=36(升),
∴还需补充的油量为:36-29=7(升)
故途中还需补充7升油.
点评 本题考查的是正数与负数的定义,解答此题的关键是熟知用正负数表示两种具有相反意义的量.具有相反意义的量都是互相依存的两个量,它包含两个要素,一是它们的意义相反,二是它们都是数量.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
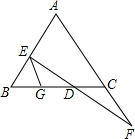 如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)
如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com