
已知:函数y=ax2﹣(3a+1)x+2a+1(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x2﹣x1=2.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
(1)a=0或﹣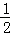 或﹣1;(2)①y=x2﹣4x+3②
或﹣1;(2)①y=x2﹣4x+3②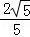 .
.
【解析】
试题分析:(1)分一次函数和二次函数两种情况讨论;(2)①根据题意可得x1,x2为ax2﹣(3a+1)x+2a+1=0的两个根,然后利用根与系数的关系,将x2﹣x1=2进行变形消去x1,x2,,解以a为未知数的方程即可;②根据条件求出点A、B、C、D的坐标,过点D作DE⊥CB于E,可证△EDB为等腰直角三角形,利用勾股定理求出DE、CD的长,根据定义可求sin∠DCB的值.
试题解析:【解析】
(1)函数y=ax2﹣(3a+1)x+2a+1(a为常数),
若a=0,则y=﹣x+1,与坐标轴有两个交点(0,1),(1,0); 1分
若a≠0且图象过原点时,2a+1=0,a=﹣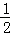 ,有两个交点(0,0),(1,0); 2分
,有两个交点(0,0),(1,0); 2分
若a≠0且图象与x轴只有一个交点时,令△=0有:
△=(3a+1)2﹣4a(2a+1)=0,解得a=﹣1,有两个交点(0,﹣1),(1,0).
综上得:a=0或﹣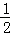 或﹣1时,函数图象与坐标轴有两个交点. 4分
或﹣1时,函数图象与坐标轴有两个交点. 4分
(2)①∵函数与x轴相交于点A(x1,0),B(x2,0)两点,
∴x1,x2为ax2﹣(3a+1)x+2a+1=0的两个根,
∴x1+x2= ,x1x2=
,x1x2=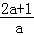 ,∵x2﹣x1=2,
,∵x2﹣x1=2,
∴4=(x2﹣x1)2=(x1+x2)2﹣4x1x2=( )2﹣4
)2﹣4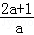 ,
,
解得a=﹣ (函数开口向上,a>0,舍去),或a=1,
(函数开口向上,a>0,舍去),或a=1,
∴y=x2﹣4x+3. 8分
②∵函数y=x2﹣4x+3与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x1<x2,
∴A(1,0),B(3,0),C(0,3),∵D为A关于y轴的对称点,∴D(﹣1,0).
根据题意画图,
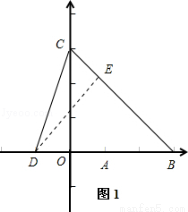
如图1,过点D作DE⊥CB于E,∵OC=3,OB=3,OC⊥OB,∴△OCB为等腰直角三角形,∴∠CBO=45°,∴△EDB为等腰直角三角形,
设DE=x,则EB=x,∵DB=4,∴x2+x2=42,∴x=2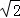 ,即DE=2
,即DE=2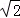 .
.
在Rt△COD中,∵DO=1,CO=3,∴CD=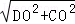 =
=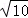 ,∴sin∠DCB=
,∴sin∠DCB=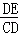 =
=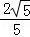 . 14分
. 14分
考点:1.函数与坐标轴的交点;2.一元二次方程根与系数的关系;3.勾股定理;4.三角函数.


科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:解答题
(本题满分10分)已知反比例函数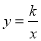 的图象与一次函数
的图象与一次函数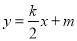 的图象交点为(2,2).
的图象交点为(2,2).
(1)求这两个函数的解析式;
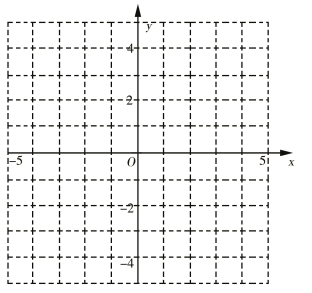
(2)在下面的坐标纸中大致画出两个函数的图象,根据图象写出不等式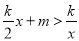 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:选择题
有一组数据:3,4,5,6,6,则下列四个结论中正确的是( )
A.这组数据的平均数、众数、中位数分别是4.8,6,6
B.这组数据的平均数、众数、中位数分别是5,5,5
C.这组数据的平均数、众数、中位数分别是4.8,6,5
D.这组数据的平均数、众数、中位数分别是5,6,6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:填空题
如图,在等边△ABC中,D是边AC上的一点,连接BD,将△BCD绕点B逆时针旋转60°,得
到△BAE,连接ED,若BC=10,BD=9,则△AED的周长是______.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
若3是关于x的方程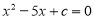 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )
A.-2 B.2 C.-5 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:解答题
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
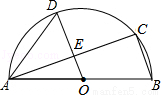
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:填空题
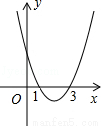
如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 _________ .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考二模数学试卷(解析版) 题型:解答题
(本题满分6分)如图,抛物线y=﹣x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
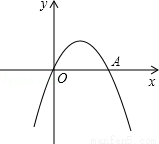
(1)求此抛物线的解析式;
(2)若抛物线上有一点B,且S△OAB=8,请直接写出点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com