
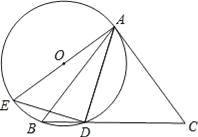
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
【答案】(1)详见解析;(2)⊙O的直径为![]() .
.
【解析】试题分析:(1)根据等腰三角形的性质,由AB=AC,AD=DC得∠C=∠B,∠1=∠C,则∠1=∠B,根据圆周角定理得∠E=∠B,∠ADE=90°,所以∠1+∠EAD=90°,然后根据切线的判定定理即可得到AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,根据等腰三角形的性质得CF=![]() AC=3,在Rt△CDF中,利用正弦定义得sinC=
AC=3,在Rt△CDF中,利用正弦定义得sinC=![]() =
=![]() ,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
试题解析:(1)∵AB=AC,AD=DC,
∴∠C=∠B,∠1=∠C,
∴∠1=∠B,
又∵∠E=∠B,
∴∠1=∠E,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠1+∠EAD=90°,即∠EAC=90°,
∴AE⊥AC,
∴AC是⊙O的切线;
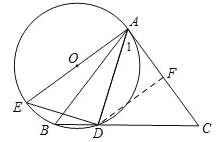
(2)过点D作DF⊥AC于点F,如图,
∵DA=DC,
∴CF=![]() AC=3,
AC=3,
在Rt△CDF中,∵sinC=![]() =
=![]() ,
,
设DF=4x,DC=5x,
∴CF=![]() =3x,
=3x,
∴3x=3,解得x=1,
∴DC=5,
∴AD=5,
∵∠ADE=∠DFC=90°,∠E=∠C,
∴△ADE∽△DFC,
∴![]() ,即
,即![]() ,解得AE=
,解得AE=![]() ,
,
即⊙O的直径为![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.
收集数据 17 18 16 12 24 15 27 25 18 19
22 17 16 19 31 29 16 14 15 25
15 31 23 17 15 15 27 27 16 19
整理、描述数据
销售额/万元 | 12 | 14 | 15 | 16 | 17 | 18 | 19 | 22 | 23 | 24 | 25 | 27 | 29 | 31 |
人数 | 1 | 1 | 4 | 3 | 2 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
分析数据 样本数据的平均数、众数、中位数如下表所示:
平均数 | 众数 | 中位数 |
20 | 18 |
得出结论 ⑴如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为 万元.
⑵如果想确定一个较高的销售目标,这个目标可以定为每月 万元,理由为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年元旦即将到来之际建湖县大润发和家乐福两超市准备提前庆祝该节日,分别推出如下促销方式:
大润发:全场均按八五折优惠;
家乐福:购物不超过200元,不给于优惠;超过了200元而不超过500元一律打八八折;超过500元时,其中的500元优惠12%,超过500元的部分打八折;
已知两家超市相同商品的标价都一样.
(1)当一次性购物总额是400元时,大润发、家乐福两家超市实付款分别是多少?
(2)当购物总额是多少时,大润发、家乐福两家超市实付款相同?
(3)某顾客在家乐福超市购物实际付款482元,试问该顾客的选择划算吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公路养护小组,乘车沿南北走向的公路巡察维护,如果规定向北为正,向南为负,某天的行驶记录如下:(单位:![]() )
)
+18,-9,+17,-14,-5,+12,-6,-7,+8,+15.
(1)养护小组最后到达的地方在出发点的哪个方向?离出发点多远?
(2)若汽车的油耗为![]() ,则这天汽车共耗油多少?
,则这天汽车共耗油多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
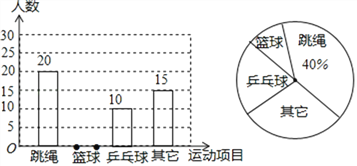
(1)在这次调查中,喜欢篮球项目的同学有多少人?
(2)在扇形统计图中,“乒乓球”的百分比为多少?
(3)如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目?
(4)请将条形统计图补充完整.
(5)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=![]() ,线段AB的中点表示的数为
,线段AB的中点表示的数为![]() .
.
(问题情境)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(综合运用)(1)点B表示的数是__________.
(2)若BC:AC=4:7,求点C到原点的距离.
(3)如图2,在(2)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(4)如图3,在(2)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒,1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT-MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com