
【题目】在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为a,则关于x的一元二次方程ax2-2ax+a+3=0有实数根的概率________;
(2)从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据方程组有实根计算出a的取值范围,再结合题意得出答案.(2)根据列表,将所有等可能的情况表示出来,再根据题意得出答案.
(1)∵方程ax2-2ax+a+3=0有实数根,
∴△=4a2-4a(a+3)=-12a≥0,且a≠0,解得 a<0,
则方程ax2-2ax+a+3=0有实数根的概率为![]() ;
;
(2)列表如下:
-3 | -1 | 0 | 2 | |
-3 | — | (-3,-1) | (0,-3) | (2,-3) |
-1 | (-3,-1) | — | (0,-1) | (2,-1) |
0 | (-3,-1) | (-1,0) | — | (2,0) |
2 | (-3,-1) | (-1,2) | (0,2) | — |
所有等可能的情况有12种,其中点(x,y)落在第二象限内的情况有2种,
则P=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如右图,O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到点P时所经过的最短路径的痕迹如图.若沿OM将圆锥侧面剪开并展平,所得侧面展开图是( )
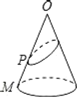
A.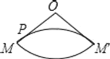 B.
B.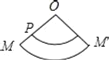
C.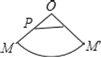 D.
D.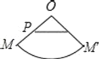
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本)
(利润=售价﹣制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
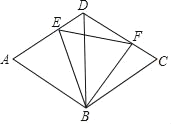
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
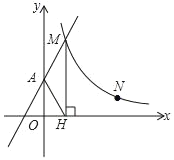
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
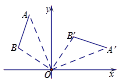
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是
A. (2,5) B. (5,2) C. (4, ![]() ) D. (
) D. (![]() ,4)
,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com