
【题目】如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
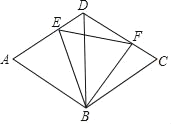
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
【答案】(1)见解析;(2)△BEF是等边三角形.理由见解析
【解析】
(1)先判定△ABD与△BCD都是等边三角形,根据等边三角形的性质可得∠BDE=∠C=60°,再求出DE=CF,然后利用“边边角”证明两三角形全等;
(2)根据全等三角形对应边相等可得BE=CF,全等三角形对应角相等可得∠DBE=∠CBF,然后求出∠EBF=60°,再根据等边三角形的判定得解,利用旋转变换解答.
(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
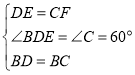 ,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF.
故答案为:(1)见解析;(2)△BEF是等边三角形.理由见解析.


科目:初中数学 来源: 题型:
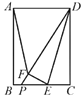
【题目】如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在探究函数y=x2﹣2|x|+3的图象和性质时,经历了以下探究过程:
(1)列表(完成下列表格).
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | 0 |
| 1 | 2 | 3 | … |
y | … | 6 | 3 | 2 |
|
|
| 2 | 3 | 6 | … |
(2)描点并在图中画出函数的大致图象;
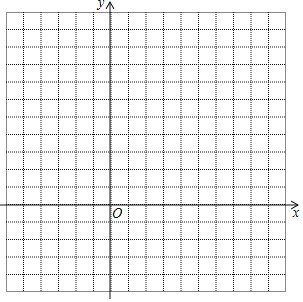
(3)根据函数图象,完成以下问题:
①观察函数y=x2﹣2|x|+3的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数y=x2﹣2|x|+3的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数y=x2﹣2|x|+3的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数y=(x﹣2)2﹣2|x﹣2|+3的图象,可以看作是函数y=x2﹣2|x|+3的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程x2﹣2|x|+3=m有四个解.
③设函数y=x2﹣2|x|+3的图象与其对称轴相交于P点,当直线y=n和函数y=x2﹣2|x|+3图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为a,则关于x的一元二次方程ax2-2ax+a+3=0有实数根的概率________;
(2)从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
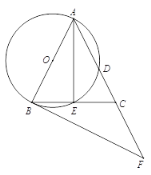
【题目】如图,在△ABC 中,AB = AC,以AB为直径的⊙O 分 别交AC,BC于点 D,E,过点B作⊙O的切线, 交 AC的延长线于点F.
(1) 求证:∠CBF =![]() ∠CAB;
∠CAB;
(2) 若CD = 2,![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (费用
(费用![]() 灯的售价
灯的售价![]() 电费,单位:元)与照明时间
电费,单位:元)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是
(小时)的函数图象,假设两种灯的使用寿命都是![]() 小时,照明效果一样.
小时,照明效果一样.
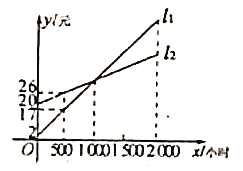
(1)根据图象分别求出![]() ,
,![]() 的函数表达式;
的函数表达式;
(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三张“黑桃”扑克牌,背面完全相同将三张扑克牌背面朝上,洗匀后放在桌面上甲,乙两人进行摸牌游戏,甲先从中随机抽取一张,记下数字再放回洗匀,乙再从中随机抽取一张.

(1)甲抽到“黑桃”,这一事件是 事件(填“不可能“,“随机“,“必然”);
(2)利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的开口向上顶点为P
的开口向上顶点为P
(1)若P点坐标为(4,一1),求抛物线的解析式;
(2)若此抛物线经过(4,一1),当-1≤x≤2时,求y的取值范围(用含a的代数式表示)
(3)若a=1,且当0≤x≤1时,抛物线上的点到x轴距离的最大值为6,求b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
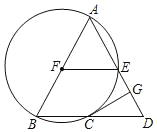
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于E,CG是⊙F的切线,CG交AD于点G.
(1)求证:CG⊥AD;
(2)填空:
①若△BDA的面积为80,则△BCF的面积为 ;
②当∠BAD的度数为 时,四边形EFCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com