
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,B点的坐标为(4,3).双曲线y= ![]() (x>0)过BC的中点P,交AB于点Q.
(x>0)过BC的中点P,交AB于点Q. 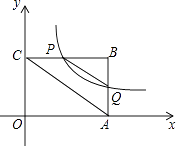
(1)求双曲线的函数表达式及点Q的坐标;
(2)判断线段AC与线段PQ之间的关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点逆时针旋转度得到的,B1的坐标是;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是线段AB的延长线,且∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥_____,根据是_____________;
(2)由∠CBE=∠C可以判断____∥_____,根据是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
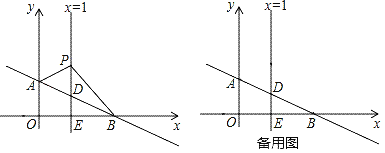
【题目】如图,平面直角坐标系中,直线AB交y轴于点A(0,1),交x轴于点B(3,0).直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,在点D的上方,设P(1,n).
(1)求直线AB的解析式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣ ![]() (x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.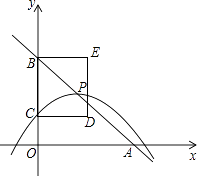
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;
(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用问题:
一个蓄水池装有甲、乙两个进水管和丙一个出水管,单独开放甲管3小时可注满一池水,单独开放乙管6小时可注满一池水,单独开放丙管4小时可放尽一池水.
(1)若同时开放甲、乙、丙三个水管,几小时可注满水池?
(2)若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需几小时可注满水池?
(3)若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管,能注满水池吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com