
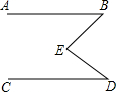
 如图.已知AB∥CD,∠B=58°,∠D=40°,求∠BED的度数.(至少用两种方法求解)
如图.已知AB∥CD,∠B=58°,∠D=40°,求∠BED的度数.(至少用两种方法求解) 分析 方法一:作EF∥AB,如图1,由于AB∥CD,则可判断AB∥EF∥CD,根据平行线的性质得∠1=∠B=58°,∠2=∠D=40°,于是得到∠BED=98°;
方法二:延长BE交CD于H,如图2,根据平行线的性质得∠1=∠B=58°,然后根据三角形外角性质计算∠BED的度数.
解答 解:方法一:作EF∥AB,如图1,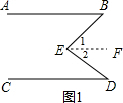
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠B=58°,∠2=∠D=40°,
∴∠BED=58°+40°=98°;
方法二:延长BE交CD于H,如图2,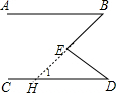
∵AB∥CD,
∴∠1=∠B=58°,
∴∠BED=∠1+∠D=58°+40°=98°.
点评 本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形外角性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 用长为8m的铝合金条做一个如图所示的矩形窗框,设水平的一边长为xcm,窗户的透光面积为ym2,那么y与x之间的函数表达式为y=-$\frac{3}{2}$x2+4x.
用长为8m的铝合金条做一个如图所示的矩形窗框,设水平的一边长为xcm,窗户的透光面积为ym2,那么y与x之间的函数表达式为y=-$\frac{3}{2}$x2+4x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
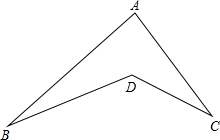 如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com