
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯB=90ЁуЃЌAB=8cmЃЌBC=6cmЃЌPЁЂQЪЧЁїABCБпЩЯЕФСНИіЖЏЕуЃЌЦфжаPЕуДгЕуAПЊЪМбиABЗНЯђдЫЖЏЧвЫйЖШЮЊУПУыlcmЃЌЕуQДгЕуBПЊЪМбиBЁњCЁњAЗНЯђдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌЫќУЧЭЌЪБГіЗЂЃЌЩшГіЗЂЕФЪБМфЮЊtУы.
(1)ГіЗЂ2УыКѓЃЌЧѓЯпЖЮPQЕФГЄ?
(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂЖљУыжгКѓЃЌOPQBЪЧЕШбќШ§НЧаЮ?
(3)ЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌЧѓФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМф?
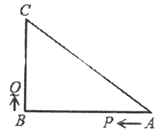
ЁОД№АИЁП(1)ГіЗЂ2УыКѓЃЌЯпЖЮPQЕФГЄЮЊ![]() ЃЛ(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ
ЃЛ(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ![]() УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ (3)ЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.
УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ (3)ЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуPЁЂQЕФдЫЖЏЫйЖШЧѓГіAPЃЌдйЧѓГіBPКЭBQЃЌгУЙДЙЩЖЈРэЧѓЕУPQМДПЩЃЛ
ЃЈ2ЃЉЩшГіЗЂtУыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃЌдђBP=BQЃЌгЩBQ=2tЃЌBP=8-tЃЌСаЪНЧѓЕУtМДПЩЃЛ
ЃЈ3ЃЉЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМфгаШ§жжЧщПіЃКЂйЕБCQ=BQЪБЃЈЭМ1ЃЉЃЌдђЁЯC=ЁЯCBQЃЌПЩжЄУїЁЯA=ЁЯABQЃЌдђBQ=AQЃЌдђCQ=AQЃЌДгЖјЧѓЕУtЃЛ
ЂкЕБCQ=BCЪБЃЈШчЭМ2ЃЉЃЌдђBC+CQ=12ЃЌвзЧѓЕУtЃЛ
ЂлЕБBC=BQЪБЃЈШчЭМ3ЃЉЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌдђЧѓГіBEЃЌCEЃЌМДПЩЕУГіtЃЎ
(1)BQ=2ЁС2=4cmЃЌBP=ABAP=82ЁС1=6cmЃЌ
ЁпЁЯB=90ЁуЃЌ
гЩЙДЙЩЖЈРэЕУЃКPQ=![]() ,
,
ЁрГіЗЂ2УыКѓЃЌЯпЖЮPQЕФГЄЮЊ![]() ЃЛ
ЃЛ
(2)BQ=2tЃЌBP=8-t ЃЌ
гЩЬтвтЕУЃК2t=8-t ЃЌ
НтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ![]() УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ
УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ
(3) ЁпЁЯABC=90ЁуЃЌBC=6ЃЌAB=8ЃЌ
ЁрAC=![]() =10.
=10.
ЂйЕБCQ=BQЪБ(ЭМ1)ЃЌдђЁЯC=ЁЯCBQЃЌ
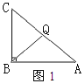
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯCBQ+ЁЯABQ=90ЁуЃЌЁЯA+ЁЯC=90ЁуЃЌ
ЁрЁЯA=ЁЯABQЃЌ
ЁрBQ=AQЃЌ
ЁрCQ=AQ=5ЃЌ
ЁрBC+CQ=11ЃЌ
Ёрt=11ЁТ2=5.5УыЃЛ
ЂкЕБCQ=BCЪБ(ШчЭМ2)ЃЌ
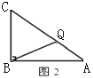
дђBC+CQ=12ЃЌ
Ёрt=12ЁТ2=6УыЃЌ
ЂлЕБBC=BQЪБ(ШчЭМ3)ЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌ
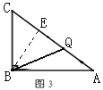
ЁрBE=![]() ЃЌ
ЃЌ
ЫљвдCE=![]() =
=![]() =3.6ЃЌ
=3.6ЃЌ
ЙЪCQ=2CE=7.2ЃЌ
ЫљвдBC+CQ=13.2ЃЌ
Ёрt=13.2ЁТ2=6.6Уы.
гЩЩЯПЩжЊЃЌЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2дкЕквЛЯѓЯоФкОЙ§ЕФећЪ§ЕуЃЈКсзјБъЁЂзнзјБъЖМЮЊећЪ§ЕФЕуЃЉвРДЮЮЊA1ЃЌA2ЃЌA3ЁAnЃЌЁЃЎНЋХзЮяЯпy=x2бижБЯпLЃКy=xЯђЩЯЦНвЦЃЌЕУвЛЯЕСаХзЮяЯпЃЌЧвТњзуЯТСаЬѕМўЃКЂйХзЮяЯпЕФЖЅЕуM1ЃЌM2ЃЌM3ЃЌЁMnЃЌЁЖМдкжБЯпLЃКy=xЩЯЃЛЂкХзЮяЯпвРДЮОЙ§ЕуA1ЃЌA2ЃЌA3ЁAnЃЌЁЃЎдђЖЅЕуM2014ЕФзјБъЮЊ_______ЃЎ
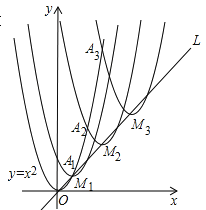
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDжаЃЌBDЁЭADЃЌЁЯA=45ЁуЃЌEЁЂFЗжБ№ЪЧABЃЌCDЩЯЕФЕуЃЌЧвBE=DFЃЌСЌНгEFНЛBDгкOЃЎ

ЃЈ1ЃЉЧѓжЄЃКBO=DOЃЛ
ЃЈ2ЃЉШєEFЁЭABЃЌбгГЄEFНЛADЕФбгГЄЯпгкGЃЌЕБFG=1ЪБЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊећЪ§![]() ТњзуЯТСаЬѕМўЃК
ТњзуЯТСаЬѕМўЃК![]() =0ЃЌ
=0ЃЌ![]() =Љ|
=Љ|![]() +1|ЃЌ
+1|ЃЌ![]() =Љ|
=Љ|![]() +2|ЃЌ
+2|ЃЌ![]() =Љ|
=Љ|![]() +3|ЃЌЁЁвдДЫРрЭЦЃЌдђ
+3|ЃЌЁЁвдДЫРрЭЦЃЌдђ![]() ЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. Љ1007 B. Љ1008 C. Љ1009 D. Љ2018
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСадЫЫуЃК81ЃН8ЃЌ82ЃН64ЃЌ83ЃН512ЃЌ84ЃН4 096ЃЌ85ЃН32 768ЃЌ86ЃН262 144ЃЌЁЃЌдђ81ЃЋ82ЃЋ83ЃЋ84ЃЋЁЃЋ82 018ЃЋ82 019ЕФКЭЕФИіЮЛЪ§зжЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫВЮМгжаПМЬхг§ВтЪдЃЌМзЁЂввЁЂБћШ§ЮЛЭЌбЇНјаазуЧђДЋЧђбЕСЗЃЌЧђДгвЛИіШЫНХЯТЫцЛњДЋЕНСэвЛИіШЫНХЯТЃЌЧвУПЮЛДЋЧђШЫДЋИјЦфгрСНШЫЕФЛњЛсЪЧОљЕШЕФЃЌгЩМзПЊЪМДЋЧђЃЌЙВДЋЧђШ§ДЮЃЎ
ЃЈ1ЃЉЧыРћгУЪїзДЭМСаОйГіШ§ДЮДЋЧђЕФЫљгаПЩФмЧщПіЃЛ
ЃЈ2ЃЉЧѓШ§ДЮДЋЧђКѓЃЌЧђЛиЕНМзНХЯТЕФИХТЪЃЛ
ЃЈ3ЃЉШ§ДЮДЋЧђКѓЃЌЧђЛиЕНМзНХЯТЕФИХТЪДѓЛЙЪЧДЋЕНввНХЯТЕФИХТЪДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЃx2ЃЋmxЕФЖдГЦжсЮЊжБЯпxЃН2ЃЌШєЙигкxЕФвЛдЊЖўДЮЗНГЬЃx2ЃЋmxЃtЃН0дк1ЃМxЃМ5ЕФЗЖЮЇФкгаНтЃЌдђtЕФШЁжЕЗЖЮЇЪЧ( )
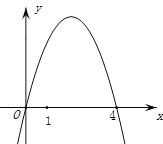
A. tЃОЃ5 B. Ѓ5ЃМtЃМ3 C. Ѓ5ЃМtЁм4 D. 3ЃМtЁм4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФвЛжЇЮЛгкЕквЛЯѓЯоЃЎ
ЕФЭМЯѓЕФвЛжЇЮЛгкЕквЛЯѓЯоЃЎ
ЃЈ1ЃЉХаЖЯИУКЏЪ§ЭМЯѓЕФСэвЛжЇЫљдкЕФЯѓЯоЃЌВЂЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШчЭМЃЌOЮЊзјБъдЕуЃЌЕуAдкИУЗДБШР§КЏЪ§ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌЕуBгыЕуAЙигк![]() жсЖдГЦЃЌШєЁїOABЕФУцЛ§ЮЊ6ЃЌЧѓmЕФжЕЃЎ
жсЖдГЦЃЌШєЁїOABЕФУцЛ§ЮЊ6ЃЌЧѓmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЙцЖЈЃКНЋШЮвтШ§ИіЛЅВЛЯрЕШЕФЪ§aЃЌbЃЌcАДееДгаЁЕНДѓЕФЫГађХХСаКѓЃЌАбДІгкжаМфЮЛжУЕФЪ§НазіетШ§ИіЪ§ЕФжаЮЛЪ§ЃЎгУЗћКХmid{aЃЌbЃЌc}БэЪОЃЎР§Шчmid{Љ1ЃЌ2ЃЌ1}ЃН1ЃЎ
ЃЈ1ЃЉmid{![]() ЃЌ5ЃЌ3}ЃНЁЁЁЁЃЎ
ЃЌ5ЃЌ3}ЃНЁЁЁЁЃЎ
ЃЈ2ЃЉЕБxЃМЉ2ЪБЃЌЧѓmid{1+xЃЌ1ЉxЃЌЉ1}ЃЎ
ЃЈ3ЃЉШєxЁй0ЃЌЧвmid{5ЃЌ5Љ2xЃЌ2x+1}ЃН2x+1ЃЌЧѓxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com