【题目】我们规定：将任意三个互不相等的数a，b，c按照从小到大的顺序排列后，把处于中间位置的数叫做这三个数的中位数．用符号mid{a，b，c}表示．例如mid{﹣1，2，1}＝1．
（1）mid{
，5，3}＝ ．
（2）当x＜﹣2时，求mid{1+x，1﹣x，﹣1}．
（3）若x≠0，且mid{5，5﹣2x，2x+1}＝2x+1，求x的取值范围．
【答案】（1）
；（2）mid{1+x，1﹣x，﹣1}＝﹣1；（3）x的取值范围是1＜x＜2．
【解析】
（1）根据中位数的定义直接得出答案；
（2）根据x＜2得出1＋x＜1，1x＞3，再进行求解即可得出答案；
（3）分两种情况讨论，当5＜2x＋1＜52x时和52x＜2x＋1＜5时，再解不等式，即可得出答案．
（1）∵5＞＞3
∴mid{，5，3}＝
故答案为：．
（2）当x＜﹣2时，1+x＜﹣1，1﹣x＞3，
∴1+x＜﹣1＜1﹣x，
∴mid{1+x，1﹣x，﹣1}＝﹣1．
（3）当5＜2x+1＜5﹣2x时，解得x＞2且x＜1，不等式组无解．
当5﹣2x＜2x+1＜5时，
解得1＜x＜2．
∴x的取值范围是1＜x＜2．
科目：初中数学 来源： 题型：
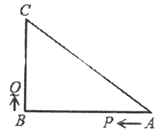
【题目】如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中P点从点A开始沿AB方向运动且速度为每秒lcm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒.
(1)出发2秒后，求线段PQ的长?
(2)当点Q在边BC上运动时，出发儿秒钟后，OPQB是等腰三角形?
(3)当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间?
查看答案和解析>>
科目：初中数学 来源： 题型：
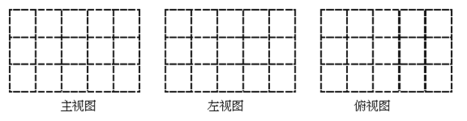
【题目】如图是由一些棱长为单位1的相同小正方体组合成的简单几何体.
（1）图中有 块小正方体；
（2）请在下面方格纸中分别画出几何体的主视图、左视图和俯视图.
（3）如果在其表面涂漆，则要涂 平方单位.（几何体放在地上，底面无法涂上漆）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面的证明．
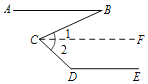
已知：如图，AB∥DE，求证：∠D+∠BCD﹣∠B＝180°．
证明：过点C作CF∥AB．
∵CF∥AB（已作），
∴∠1＝ ．
∵∠2＝∠BCD﹣∠1，
∴∠2＝∠BCD﹣∠B ．
∵AB∥DE，CF∥AB（已知），
∴CF∥DE
∴∠D+∠2＝180°
∴∠D+∠BCD﹣∠B＝180° ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
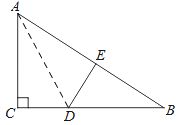
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，A(a，0)，B(0，b)，C（-a，0），且
+b2-4b+4=0．
(1)求证：∠ABC=90°；
(2)∠ABO的平分线交x轴于点D，求D点的坐标．
(3)如图，在线段AB上有两动点M、N满足∠MON=45°，求证：BM2+AN2=MN2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常繁琐，且易出错．聪明的小高斯经过探索后，给出了下面漂亮的解答过程．
解：设S＝1+2+3+…+100 ①
则S＝100+99+98+…+1 ②
①+②，得（即左右两边分别相加）：
2S＝（1+100）+（2+99）+（3+98）+…+（100+1），
＝
，
＝100×101，
所以，S＝
③，
所以，1+2+3+…+100＝5050．
后来人们将小高斯的这种解答方法概括为“倒序相加法”．请你利用“倒序相加法”解答下面的问题．
（1）计算：1+2+3+…+101；
（2）请你观察上面解答过程中的③式及你运算过程中出现的类似③式，猜想：1+2+3+…+n＝ ；
（3）至少用两种方法计算：1001+1002+…+2000．
方法1：
方法2：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
