
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB=OB,E为AC上一点,BE平分∠ABO,EF⊥BC于点F,∠CAD=45°,EF交BD于点P,BP=![]() ,则BC的长为_______.
,则BC的长为_______.
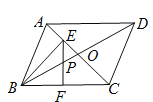
【答案】4
【解析】
过点E作EM∥AD,由△ABO是等腰三角形,根据三线合一可知点E是AO的中点,可证得EM=![]() AD=
AD=![]() BC,根据已知可求得∠CEF=∠ECF=45°,从而得∠BEF=45°,△BEF为等腰直角三角形,可得BF=EF=FC=
BC,根据已知可求得∠CEF=∠ECF=45°,从而得∠BEF=45°,△BEF为等腰直角三角形,可得BF=EF=FC=![]() BC,因此可证明△BFP≌△MEP(AAS),则EP=FP=
BC,因此可证明△BFP≌△MEP(AAS),则EP=FP=![]() FC,在Rt△BFP中,利用勾股定理可求得x,即得答案.
FC,在Rt△BFP中,利用勾股定理可求得x,即得答案.
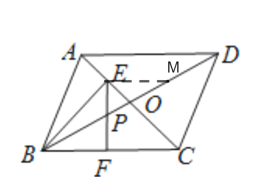
过点E作EM∥AD,交BD于M,设EM=x,
∵AB=OB,BE平分∠ABO,
∴△ABO是等腰三角形,点E是AO的中点,BE⊥AO,∠BEO=90°,
∴EM是△AOD的中位线,
又∵ABCD是平行四边形,
∴BC=AD=2EM=2x,
∵EF⊥BC, ∠CAD=45°,AD∥BC,
∴∠BCA=∠CAD=45°,∠EFC=90°,
∴△EFC为等腰直角三角形,
∴EF=FC,∠FEC=45°,
∴∠BEF=90°-∠FEC=45°,
则△BEF为等腰直角三角形,
∴BF=EF=FC=![]() BC=x,
BC=x,
∵EM∥BF,
∴∠EMP=∠FBP,∠PEM=∠PFB=90°,EM=BF,
则△BFP≌△MEP(ASA),
∴EP=FP=![]() EF=
EF=![]() FC=
FC=![]() x,
x,
∴在Rt△BFP中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
∴BC=2![]() =4,
=4,
故答案为:4.


科目:初中数学 来源: 题型:
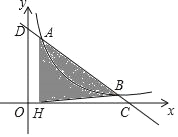
【题目】如图,直线y=![]() x+m交双曲线y=
x+m交双曲线y=![]() (x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于点H,连结BH,若OH:HC=1:5,S△ABH=1,则k的值为( )
(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于点H,连结BH,若OH:HC=1:5,S△ABH=1,则k的值为( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上
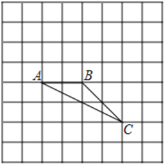
(1) 填空∠ABC=___________
(2) 若点A在网格所在的坐标平面内的坐标为(1,-2),请建立平面直角坐标系,D是平面直角坐标系中一点,并作出以A、B、C、D四个点为顶点的平行四边形,直接写出满足条件的D点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E、F分别在AD、CD上,AF、BE相交于点G,且AF=BE,则下列结论不正确的是:( )
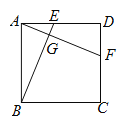
A.AF⊥BEB.BG=GFC.AE=DFD.∠EBC=∠AFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
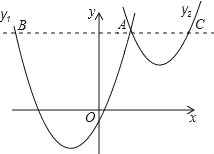
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O是对角线AC的中点.将ABCD绕点B顺时针旋转90°.旋转后的四边形为A'B′C′D',点A,C,D,O的对应点分别为A′,C',D',O’,若AB=8,BC=10,则线段CO’的长为_____.
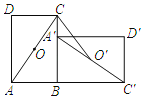
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com