
【题目】性质探究
如图①,在等腰三角形![]() 中,
中,![]() ,则底边
,则底边![]() 与腰
与腰![]() 的长度之比为________.
的长度之比为________.
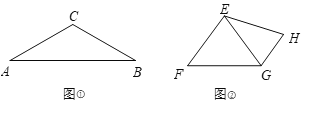
理解运用
⑴若顶角为120°的等腰三角形的周长为![]() ,则它的面积为________;
,则它的面积为________;
⑵如图②,在四边形![]() 中,
中,![]() .
.
①求证:![]() ;
;
②在边![]() 上分别取中点
上分别取中点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
类比拓展
顶角为![]() 的等腰三角形的底边与一腰的长度之比为________(用含
的等腰三角形的底边与一腰的长度之比为________(用含![]() 的式子表示).
的式子表示).
【答案】性质探究:![]() ;理解运用:(1)
;理解运用:(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() ;类比拓展:
;类比拓展:![]() .
.
【解析】
性质探究:作CD⊥AB于D,则∠ADC=∠BDC=90°,由等腰三角形的性质得出AD=BD,∠A=∠B=30°,由直角三角形的性质得出AC=2CD,AD=![]() CD,得出AB=2AD=2
CD,得出AB=2AD=2![]() CD,即可得出结果;
CD,即可得出结果;
理解运用:(1)同上得出则AC=2CD,AD=![]() CD,由等腰三角形的周长得出4CD+2
CD,由等腰三角形的周长得出4CD+2![]() CD=8+4
CD=8+4![]() ,解得:CD=2,得出AB=4
,解得:CD=2,得出AB=4![]() ,由三角形面积公式即可得出结果;
,由三角形面积公式即可得出结果;
(2)①由等腰三角形的性质得出∠EFG=∠EGF,∠EGH=∠EHG,得出∠EFG+∠EHG=∠EGF+∠EGH=∠FGH即可;
②连接FH,作EP⊥FH于P,由等腰三角形的性质得出PF=PH,由①得:∠EFG+∠EHG=∠FGH=120°,由四边形内角和定理求出∠FEH=120°,由等腰三角形的性质得出∠EFH=30°,由直角三角形的性质得出PE=![]() EF=5,PF=
EF=5,PF=![]() PE=5
PE=5![]() ,得出FH=2PF=10
,得出FH=2PF=10![]() ,证明MN是△FGH的中位线,由三角形中位线定理即可得出结果;
,证明MN是△FGH的中位线,由三角形中位线定理即可得出结果;
类比拓展:作AD⊥BC于D,由等腰三角形的性质得出BD=CD,∠BAD=![]() ∠BAC=α,由三角函数得出BD=AB×sinα,得出BC=2BD=2AB×sinα,即可得出结果.
∠BAC=α,由三角函数得出BD=AB×sinα,得出BC=2BD=2AB×sinα,即可得出结果.
性质探究
解:作CD⊥AB于D,如图①所示:
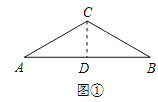
则∠ADC=∠BDC=90°,
∵AC=BC,∠ACB=120°,
∴AD=BD,∠A=∠B=30°,
∴AC=2CD,AD=![]() CD,
CD,
∴AB=2AD=2![]() CD,
CD,
∴![]() =
=![]() ;
;
故答案为:![]() ;
;
理解运用
(1)解:如图①所示:
同上得:AC=2CD,AD=![]() CD,
CD,
∵AC+BC+AB=8+4![]() ,
,
∴4CD+2![]() CD=8+4
CD=8+4![]() ,
,
解得:CD=2,
∴AB=4![]() ,
,
∴△ABC的面积=![]() AB×CD=
AB×CD=![]() ×4
×4![]() ×2=4
×2=4![]() ;
;
故答案为:4![]()
(2)①证明:∵EF=EG=EH,
∴∠EFG=∠EGF,∠EGH=∠EHG,
∴∠EFG+∠EHG=∠EGF+∠EGH=∠FGH;
②解:连接FH,作EP⊥FH于P,如图②所示:
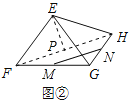
则PF=PH,由①得:∠EFG+∠EHG=∠FGH=120°,
∴∠FEH=360°-120°-120°=120°,
∵EF=EH,
∴∠EFH=30°,
∴PE=![]() EF=5,
EF=5,
∴PF=![]() PE=5
PE=5![]() ,
,
∴FH=2PF=10![]() ,
,
∵点M、N分别是FG、GH的中点,
∴MN是△FGH的中位线,
∴MN=![]() FH=5
FH=5![]() ;
;
类比拓展
解:如图③所示:作AD⊥BC于D,
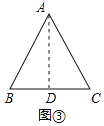
∵AB=AC,
∴BD=CD,∠BAD=![]() ∠BAC=α,
∠BAC=α,
∵sinα=![]() ,
,
∴BD=AB×sinα,
∴BC=2BD=2AB×sinα,
∴![]() =2sinα;
=2sinα;
故答案为:2sinα.


科目:初中数学 来源: 题型:
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
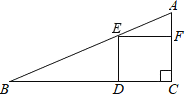
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 函数图象位于第一、三象限
B. 函数值y随x的增大而减小
C. 若A(-1,y1)、B(1,y2)、C(2,y3)是图象上三个点,则y1<y3<y2
D. P为图象上任意一点,过P作PQ⊥y轴于Q,则△OPQ的面积是定值
查看答案和解析>>
科目:初中数学 来源: 题型:
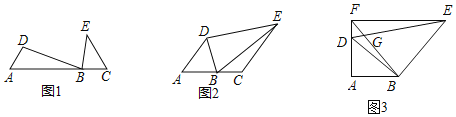
【题目】如图,∠A=∠DBE=α,
(1)如图1,若C点在射线AB上,且∠C=α,求证:![]() ;
;
(2)如图2,若C在射线AB上,α=60°,∠ABD=75°,EC∥AD,EC=2AB=4,求S四边形BCED;
(3)如图3,若α=90°,BD平分∠ADE,EF⊥AD于F,线段BF、DE交于G,若![]() ,直接写出
,直接写出![]() 的值(用含m,n的式子表示).
的值(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,当点![]() 运动到
运动到![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,分别交
,分别交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
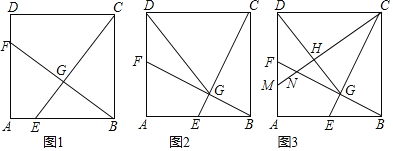
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜.某超市看好甲、乙两种有机蔬菜的市场价值,经调查,这两种蔬菜的进价和售价如下表所示:
有机蔬菜种类 | 进价(元/ | 售价(元/ |
甲 |
| 16 |
乙 |
| 18 |
(1)该超市购进甲种蔬菜10![]() 和乙种蔬菜5
和乙种蔬菜5![]() 需要170元;购进甲种蔬菜6
需要170元;购进甲种蔬菜6![]() 和乙种蔬菜10
和乙种蔬菜10![]() 需要200元.求
需要200元.求![]() ,
,![]() 的值;
的值;
(2)该超市决定每天购进甲、乙两种蔬菜共100![]() 进行销售,其中甲种蔬菜的数量不少于20
进行销售,其中甲种蔬菜的数量不少于20![]() ,且不大于70
,且不大于70![]() .实际销售时,由于多种因素的影响,甲种蔬菜超过60
.实际销售时,由于多种因素的影响,甲种蔬菜超过60![]() 的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完.求超市当天售完这两种蔬菜获得的利润额
的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完.求超市当天售完这两种蔬菜获得的利润额![]() (元)与购进甲种蔬菜的数量
(元)与购进甲种蔬菜的数量![]() (
(![]() )之间的函数关系式,并写出
)之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,超市在获得的利润额![]() (元)取得最大值时,决定售出的甲种蔬菜每千克捐出
(元)取得最大值时,决定售出的甲种蔬菜每千克捐出![]() 元,乙种蔬菜每千克捐出
元,乙种蔬菜每千克捐出![]() 元给当地福利院,若要保证捐款后的盈利率不低于20%,求
元给当地福利院,若要保证捐款后的盈利率不低于20%,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
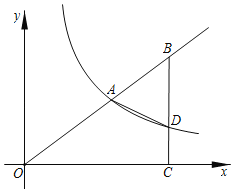
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与反比例函数的图象相交于点
与反比例函数的图象相交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求该反比例函数的解析式;
(2)若![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
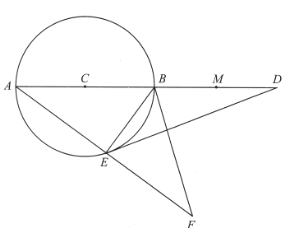
【题目】如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED=![]() .
.
(1)求证:△DEB∽△DAE;
(2)求DA,DE的长;
(3)若点F在B、E、M三点确定的圆上,求MD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com