
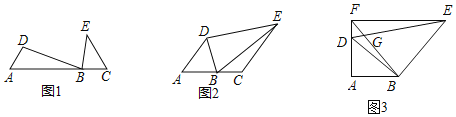
【题目】如图,∠A=∠DBE=α,
(1)如图1,若C点在射线AB上,且∠C=α,求证:![]() ;
;
(2)如图2,若C在射线AB上,α=60°,∠ABD=75°,EC∥AD,EC=2AB=4,求S四边形BCED;
(3)如图3,若α=90°,BD平分∠ADE,EF⊥AD于F,线段BF、DE交于G,若![]() ,直接写出
,直接写出![]() 的值(用含m,n的式子表示).
的值(用含m,n的式子表示).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1,证明△DAB∽△BCE,可解答;
(2)如图2,作辅助线,构建30°的直角三角形和等腰直角三角形,分别计算BE、DH、BC和EF的长,根据S四边形BCED=S△BDE+S△BCE可解答;
(3)如图3,作辅助线,构建相似三角形,证明△EFD∽△HAD和△EFG∽△HBG,列比例式可解答.
(1)证明:如图1,

∵∠A=∠DBE=α,
∴∠D+∠ABD=∠ABD+∠EBC=180°-α,
∴∠D=∠EBC,
∵∠A=∠C=α,
∴△DAB∽△BCE,
∴![]() ;
;
(2)解:如图2,过B作BG⊥AD于G,过D作DH⊥BE于H,过E作EF⊥AC于F,

∵∠DAB=60°,∠ABD=75°,
∴∠ADB=180°-60°-75°=45°,
Rt△ABG中,∠ABG=30°,AB=2,
∴AG=1,BG=![]() ,
,
∵△BDG是等腰直角三角形,
∴BD=![]() BG=
BG=![]() ,
,
∵∠DBE=α=60°,
Rt△DBH中,∠BDH=30°,
∴![]() ,
,
∵∠ABD=75°,∠DBE=60°,
∴∠EBF=45°,
∴△EBF是等腰直角三角形,
∵EC∥AD,
∴∠ECF=∠A=60°,
Rt△ECF中,∠CEF=30°,
∵EC=4,
∴CF=2,EF=BF=2![]() ,
,
∴BE=![]() EF=2
EF=2![]() ;
;
∴S四边形BCED=S△BDE+S△BCE
=![]() ;
;
(3)解:如图3,过B作BM⊥DE于M,过E作EC⊥AB于C,延长ED、BA交于H,
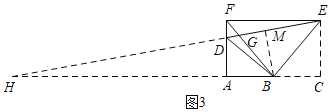
∵BD平分∠ADE,∠DAB=90°,
∴AB=BM,
∵∠DBE=α=90°,
∴∠CBE+∠ABD=∠ABD+∠ADB=90°,
∴∠CBE=∠ADB=∠BDE,
∵∠DBE=∠C=90°,
∴∠DEB=∠CEB,
∴BM=BC,
∴BC=AB,
∵EF⊥AD,
∴∠EFA=90°,
∵∠FAC=∠C=90°,
∴四边形FACE是矩形,
∴EF=AC,
设AB=x,则EF=2x,
∵EF∥CH,
∴△EFD∽△HAD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵EF∥BH,
∴△EFG∽△HBG,
∴ .
.


科目:初中数学 来源: 题型:
【题目】以下四个命题:![]() 用换元法解分式方程
用换元法解分式方程![]() 时,如果设
时,如果设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ;
;![]() 如果半径
如果半径![]() 为的圆的内接正五边形的边长为
为的圆的内接正五边形的边长为![]() ,那么
,那么![]() ;
;![]() 有一个圆锥,与底面圆直径是
有一个圆锥,与底面圆直径是![]() 且体积为
且体积为![]() 的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为
的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为![]() ;④二次函数
;④二次函数![]() ,自变量的两个值
,自变量的两个值![]() 对应的函数值分别为
对应的函数值分别为![]() ,若
,若![]() ,则
,则![]() .其中正确的命题的个数为( )
.其中正确的命题的个数为( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止.甲、乙两车相距的路程
地,两车分别到达目的地后停止.甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时,![]() ,
,![]() .
.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲车到达距![]() 地70千米处时,求甲、乙两车之间的路程.
地70千米处时,求甲、乙两车之间的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
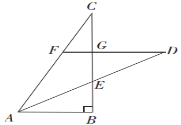
【题目】如图,在△ABC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的平分线,与BC相交于点E,点G是BC上一点,E为线段BG的中点,DG⊥BC于点G,交AC于点F,则FG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
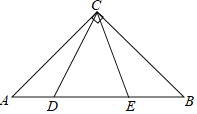
【题目】如图,在等腰直角三角形△ABC中,AC=6![]() ,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】性质探究
如图①,在等腰三角形![]() 中,
中,![]() ,则底边
,则底边![]() 与腰
与腰![]() 的长度之比为________.
的长度之比为________.
理解运用
⑴若顶角为120°的等腰三角形的周长为![]() ,则它的面积为________;
,则它的面积为________;
⑵如图②,在四边形![]() 中,
中,![]() .
.
①求证:![]() ;
;
②在边![]() 上分别取中点
上分别取中点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
类比拓展
顶角为![]() 的等腰三角形的底边与一腰的长度之比为________(用含
的等腰三角形的底边与一腰的长度之比为________(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.
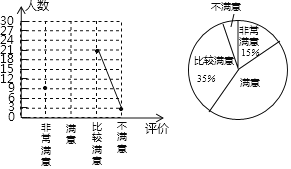
根据统计图:
(1)求该校被调查的学生总数及评价为“满意”的人数;
(2)补全折线统计图;
(3)根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
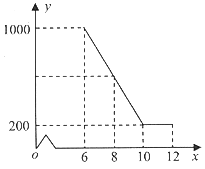
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
(1)求y与x的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com