
【题目】以下四个命题:![]() 用换元法解分式方程
用换元法解分式方程![]() 时,如果设
时,如果设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ;
;![]() 如果半径
如果半径![]() 为的圆的内接正五边形的边长为
为的圆的内接正五边形的边长为![]() ,那么
,那么![]() ;
;![]() 有一个圆锥,与底面圆直径是
有一个圆锥,与底面圆直径是![]() 且体积为
且体积为![]() 的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为
的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为![]() ;④二次函数
;④二次函数![]() ,自变量的两个值
,自变量的两个值![]() 对应的函数值分别为
对应的函数值分别为![]() ,若
,若![]() ,则
,则![]() .其中正确的命题的个数为( )
.其中正确的命题的个数为( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】D
【解析】
①利用换元法代入并化简;
②作OF⊥BC,在Rt△OCF中,利用三角函数求出a的长;
③这个圆锥母线长为R,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到![]() ,然后解关于R的方程即可;
,然后解关于R的方程即可;
④根据二次函数图象的性质和绝对值的意义进行判断可得出正确的结论.
解:![]() 设
设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ,故正确;
,故正确;
![]() 作
作![]() .
.

∵∠COF=72°÷2=36°,
∴CF=rsin36°,
∴CB=2rsin36°,即a=2rsin36°=2rcos54°.
故正确;
③设圆锥的高为h,底面半径为r,母线长为R,
根据题意得![]() ,
,
则R:r=2:1.
由 得到
得到![]()
所以h2+r2=R2,即 ,则
,则![]()
即它的母线长是![]()
故正确;
④二次函数y=ax2-2ax+1的对称轴是x=1,所以![]() 表示自变量为x时,对应点离对称轴的距离。
表示自变量为x时,对应点离对称轴的距离。
当a<0时图象开口向下,由下图可知对应点离对称轴越远所对应的函数值越小。
∵![]()
∴y1<y2
所以a(y1-y2)>0.
当a>0时图象开口向上,对应点离对称轴越远所对应的函数值越大。
∵![]()
∴y1>y2
所以a(y1-y2)>0.
故本命题正确.
综上所述,正确的命题的个数为4个.
故选:D.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
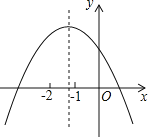
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧![]() 上取一点D,使
上取一点D,使![]() ,将△ADC沿AD对折,得到△ADE,连接CE.
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE![]() C D,劣弧
C D,劣弧![]() 的弧长为π,求⊙O的半径.
的弧长为π,求⊙O的半径.
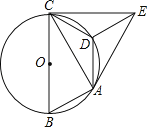
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
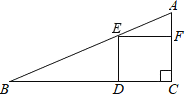
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
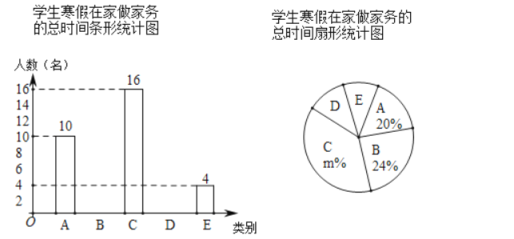
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了迎接“双11”节,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件. 设每件降价x元:
(1)降价后每件利润 元,商场能售出 件.
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
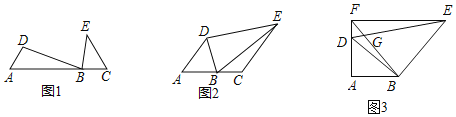
【题目】如图,∠A=∠DBE=α,
(1)如图1,若C点在射线AB上,且∠C=α,求证:![]() ;
;
(2)如图2,若C在射线AB上,α=60°,∠ABD=75°,EC∥AD,EC=2AB=4,求S四边形BCED;
(3)如图3,若α=90°,BD平分∠ADE,EF⊥AD于F,线段BF、DE交于G,若![]() ,直接写出
,直接写出![]() 的值(用含m,n的式子表示).
的值(用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com