
【题目】如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧![]() 上取一点D,使
上取一点D,使![]() ,将△ADC沿AD对折,得到△ADE,连接CE.
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE![]() C D,劣弧
C D,劣弧![]() 的弧长为π,求⊙O的半径.
的弧长为π,求⊙O的半径.
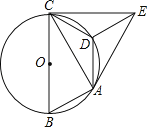
【答案】(1)见解析;(2)圆的半径为3.
【解析】
(1)在△ACE中,根据三角形内角和为180°,则2α+2β+2γ=180°,即可求解;
(2)证明四边形AMCN为矩形,![]() ,而AB=x,则
,而AB=x,则
sin∠ABM=![]() ,即∠ABM=60°,即可求解.
,即∠ABM=60°,即可求解.
(1)∵![]() ,∴∠CAD=∠BCA=α=∠EAD,
,∴∠CAD=∠BCA=α=∠EAD,
设:∠DCA=∠DEA=β,∠DCE=∠DEC=γ,
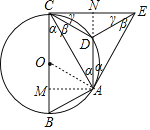
则△ACE中,根据三角形内角和为180°,
∴2α+2β+2γ=180°,
∴α+β+γ=90°,
∴CE是⊙O的切线;
(2)过点A作AM⊥BC,延长AD交CE于点N,
则DN⊥CE,∴四边形AMCN为矩形,
设:AB=CD=x,则CE![]() x,
x,
则CN![]() CE
CE![]() x=AM,而AB=x,
x=AM,而AB=x,
则sin∠ABM![]() ,∴∠ABM=60°,
,∴∠ABM=60°,
∴△OAB为等边三角形,即∠AOB=60°,
![]() 2πr=π,
2πr=π,
解得:r=3,
故圆的半径为3.


科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动.动点
匀速运动.动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 同时停止运动.设运动时间为以
同时停止运动.设运动时间为以![]() .过点
.过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 边于
边于![]() .以
.以![]() 为边作平行四边形
为边作平行四边形![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
(2)是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的平分线上?若存在,求出
的平分线上?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求![]() 的长;
的长;
(4)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,得
翻折,得![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的值最小?并求出最小值.
的值最小?并求出最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.
(1)求购买甲、乙两种树苗各多少棵?
(2)为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
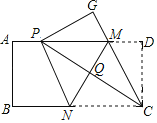
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是甲、乙两名同学近五次数学测试(满分均为100分)的成绩统计表:
同学 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲 | 90 | 88 | 92 | 94 | 91 |
乙 | 90 | 91 | 93 | 94 | 92 |
根据上表数据,成绩较好且比较稳定的同学是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:![]() 用换元法解分式方程
用换元法解分式方程![]() 时,如果设
时,如果设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ;
;![]() 如果半径
如果半径![]() 为的圆的内接正五边形的边长为
为的圆的内接正五边形的边长为![]() ,那么
,那么![]() ;
;![]() 有一个圆锥,与底面圆直径是
有一个圆锥,与底面圆直径是![]() 且体积为
且体积为![]() 的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为
的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为![]() ;④二次函数
;④二次函数![]() ,自变量的两个值
,自变量的两个值![]() 对应的函数值分别为
对应的函数值分别为![]() ,若
,若![]() ,则
,则![]() .其中正确的命题的个数为( )
.其中正确的命题的个数为( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
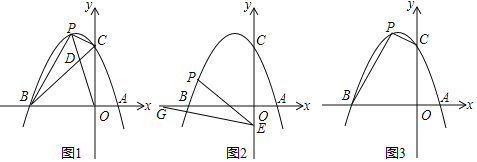
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和直线
和直线![]() 都经过点
都经过点![]() ,点
,点![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线上的动点,直线
为抛物线上的动点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)当![]() 是以
是以![]() 为底边的等腰三角形时,求点
为底边的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)满足(2)的条件时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形△ABC中,AC=6![]() ,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
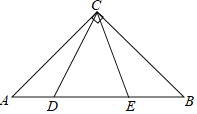
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com