
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
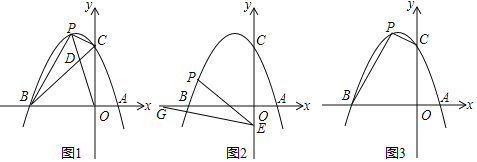
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3,顶点坐标为(﹣1,4);(2)点D(﹣1,2);(3)点P(![]() ,
,![]() )(4)不存在,理由见解析.
)(4)不存在,理由见解析.
【解析】
(1)利用待定系数法可求得函数的表达式,再通过配方即可求得顶点坐标;
(2)又S△CPD:S△BPD=1:2,可得BD=![]() BC=
BC=![]() ×
×![]() =
=![]() ,再利用解直角三角形的知识即可求得答案;
,再利用解直角三角形的知识即可求得答案;
(3)设直线PE交x轴于点H,∠OGE=15°,∠PEG=2∠OGE=30°,则∠OHE=45°,故OH=OE=1,解由①②构成的方程组即可求得答案;
(4)连接BC,过点P作y轴的平行线交BC于点H,设点P(x,﹣x2﹣2x+3),点H(x,x+3),则S四边形BOCP=S△OBC+S△PBC=![]() ×3×3+
×3×3+![]() (﹣x2﹣2x+3﹣x﹣3)×3=8,得到关于x的一元二次方程,根据方程解的情况即可得结论.
(﹣x2﹣2x+3﹣x﹣3)×3=8,得到关于x的一元二次方程,根据方程解的情况即可得结论.
(1)∵抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),
∴![]() ,
,
∴![]() ,
,
∴抛物线的表达式为:y=﹣x2﹣2x+3…①,
y=﹣x2﹣2x+3=-(x+1)2+4,
∴顶点坐标为(﹣1,4);
(2)设点D坐标为(xD,yD),∵OB=OC,∠BOC=90°,
∴∠CBO=45°,BC=![]() ,
,
∵S△CPD:S△BPD=1:2,
∴BD:DC=2:1,
∴BD=![]() BC=
BC=![]() ×
×![]() =
=![]() ,
,
∴xD=-3+ BDcos∠CBO=-3+2=-1, yD=BDsin∠CBO=2,
∴点D(﹣1,2);
(3)如图2,设直线PE交x轴于点,
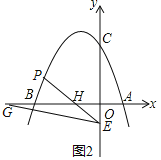
∵∠OGE=15°,∠EOG=90°,
∴∠OEG=90°-15°=75°,
∵∠PEG=2∠OGE,
∴∠PEG=2∠OGE=30°,
∴∠OHE=∠OGE+∠PEG=45°,∠HEO=∠OEG-∠PEG=45°,
∴OH=OE=1,
∴H(-1,0),
设直线HE的解析式为y=mx+n,把H(-1,0)、E(0,-1)分别代入得![]() ,
,
解得![]() ,
,
∴直线HE的表达式为:y=﹣x﹣1…②,
联立①②并解得: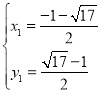 ,
,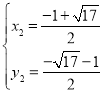 (舍去),
(舍去),
故点P(![]() ,
,![]() );
);
(4)不存在,理由:
如图3,连接BC,过点P作y轴的平行线交BC于点H,
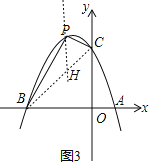
直线BC的表达式为:y=x+3,
设点P(x,﹣x2﹣2x+3),点H(x,x+3),
则S四边形BOCP=S△OBC+S△PBC=![]() ×3×3+
×3×3+![]() (﹣x2﹣2x+3﹣x﹣3)×3=8,
(﹣x2﹣2x+3﹣x﹣3)×3=8,
整理得:3x2+9x+7=0,
解得:△<0,故方程无解,
则不存在满足条件的点P.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:①abc<0;②c+2a>0;③9a﹣3b+c=0;④a﹣b≤am2+bm(m为实数);⑤4ac﹣b2<0.其中正确结论的个数是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
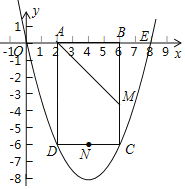
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
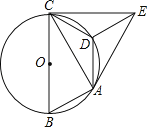
【题目】如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧![]() 上取一点D,使
上取一点D,使![]() ,将△ADC沿AD对折,得到△ADE,连接CE.
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE![]() C D,劣弧
C D,劣弧![]() 的弧长为π,求⊙O的半径.
的弧长为π,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
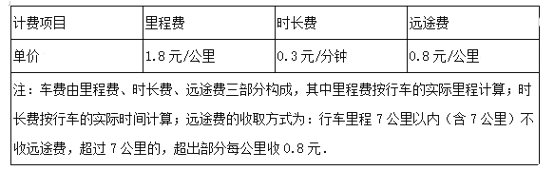
小王与小张各自乘坐满滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为![]() 公里与
公里与![]() 公里,两人付给滴滴快车的乘车费相同.
公里,两人付给滴滴快车的乘车费相同.
![]() 求这两辆滴滴快车的实际行车时间相差多少分钟;
求这两辆滴滴快车的实际行车时间相差多少分钟;
![]() 实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的
实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的![]() 倍,且比另一人的实际乘车时间的一半多
倍,且比另一人的实际乘车时间的一半多![]() 分钟,计算俩人各自的实际乘车时间.
分钟,计算俩人各自的实际乘车时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
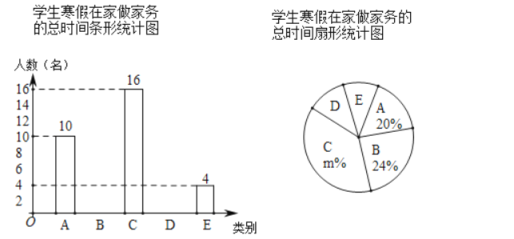
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF∥BE,过点C作CG⊥AB交AB的延长线于点G.
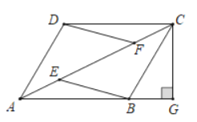
(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=![]() ,∠CBG=45°,BC=4
,∠CBG=45°,BC=4![]() ,则ABCD的面积是 .
,则ABCD的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
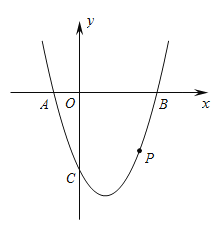
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com