
ΓΨΧβΡΩΓΩΒΈΒΈΩλ≥Β «“Μ÷÷±ψΫίΒΡ≥ω––ΙΛΨΏΘ§ΦΤΦέΙφ‘ρ»γœ¬±μΘΚ
–ΓΆθ”κ–Γ’≈ΗςΉ‘≥ΥΉχ¬ζΒΈΩλ≥ΒΘ§‘ΎΆ§“ΜΒΊΒψ‘ΦΦϊΘ§“―÷ΣΒΫ¥ο‘ΦΦϊΒΊΒψ ±ΥϊΟ«ΒΡ ΒΦ ––≥Βάο≥ΧΖ÷±πΈΣ![]() ΙΪάο”κ
ΙΪάο”κ![]() ΙΪάοΘ§ΝΫ»ΥΗΕΗχΒΈΒΈΩλ≥ΒΒΡ≥Υ≥ΒΖ―œύΆ§Θ°
ΙΪάοΘ§ΝΫ»ΥΗΕΗχΒΈΒΈΩλ≥ΒΒΡ≥Υ≥ΒΖ―œύΆ§Θ°
![]() «σ’βΝΫΝΨΒΈΒΈΩλ≥ΒΒΡ ΒΦ ––≥Β ±Φδœύ≤νΕύ…ΌΖ÷÷”ΘΜ
«σ’βΝΫΝΨΒΈΒΈΩλ≥ΒΒΡ ΒΦ ––≥Β ±Φδœύ≤νΕύ…ΌΖ÷÷”ΘΜ
![]() ΒΦ ≥Υ≥Β ±ΦδΫœ…ΌΒΡ»ΥΘ§”…”Ύ≥ωΖΔ ±Φδ±»Νμ“Μ»Υ‘γΘ§Υυ“‘Χα«ΑΒΫ¥ο‘ΦΦϊΒΊΒψ‘Ύ¥σΧϋΒ»ΚρΘ°“―÷ΣΥϊΒ»ΚρΝμ“Μ»ΥΒΡ ±Φδ «ΥϊΉ‘ΦΚ ΒΦ ≥Υ≥Β ±ΦδΒΡ
ΒΦ ≥Υ≥Β ±ΦδΫœ…ΌΒΡ»ΥΘ§”…”Ύ≥ωΖΔ ±Φδ±»Νμ“Μ»Υ‘γΘ§Υυ“‘Χα«ΑΒΫ¥ο‘ΦΦϊΒΊΒψ‘Ύ¥σΧϋΒ»ΚρΘ°“―÷ΣΥϊΒ»ΚρΝμ“Μ»ΥΒΡ ±Φδ «ΥϊΉ‘ΦΚ ΒΦ ≥Υ≥Β ±ΦδΒΡ![]() ±ΕΘ§«“±»Νμ“Μ»ΥΒΡ ΒΦ ≥Υ≥Β ±ΦδΒΡ“ΜΑκΕύ
±ΕΘ§«“±»Νμ“Μ»ΥΒΡ ΒΦ ≥Υ≥Β ±ΦδΒΡ“ΜΑκΕύ![]() Ζ÷÷”Θ§ΦΤΥψΝ©»ΥΗςΉ‘ΒΡ ΒΦ ≥Υ≥Β ±ΦδΘ°
Ζ÷÷”Θ§ΦΤΥψΝ©»ΥΗςΉ‘ΒΡ ΒΦ ≥Υ≥Β ±ΦδΘ°
ΓΨ¥πΑΗΓΩ(1) ’βΝΫΝΨΒΈΒΈΩλ≥ΒΒΡ ΒΦ ––≥Β ±Φδœύ≤ν![]() Ζ÷÷”Θ°(2) –ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣ
Ζ÷÷”Θ°(2) –ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ
Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ°
Ζ÷÷”Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…η–ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣxΖ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣyΖ÷÷”Θ§ΗυΨίΝΫ»ΥΗΕΗχΒΈΒΈΩλ≥ΒΒΡ≥Υ≥ΒΖ―œύΆ§Ν–ΖΫ≥Χ«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΓΑΒ»ΚρΝμ“Μ»ΥΒΡ ±Φδ «ΥϊΉ‘ΦΚ ΒΦ ≥Υ≥Β ±ΦδΒΡ1.5±ΕΘ§«“±»Νμ“Μ»ΥΒΡ ΒΦ ≥Υ≥Β ±ΦδΒΡ“ΜΑκΕύ8.5Ζ÷÷”Γ±Ν–Εΰ‘Σ“Μ¥ΈΖΫ≥ΧΘ§ΫΪΤδ”κΘ®1Θ©÷–ΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΝΣΝΔΦ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©…η–ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ
Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ§”…Χβ“βΒΟΘΚ
Ζ÷÷”Θ§”…Χβ“βΒΟΘΚ
![]()
![]()
![]()
![]()
![]() ’βΝΫΝΨΒΈΒΈΩλ≥ΒΒΡ ΒΦ ––≥Β ±Φδœύ≤ν
’βΝΫΝΨΒΈΒΈΩλ≥ΒΒΡ ΒΦ ––≥Β ±Φδœύ≤ν![]() Ζ÷÷”Θ°
Ζ÷÷”Θ°
Θ®2Θ©”…Θ®1Θ©ΦΑΧβ“βΒΟΘΚ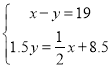
Μ·ΦρΒΟ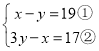
![]() ΒΟ
ΒΟ![]()
![]()
ΫΪ![]() ¥ζ»κ
¥ζ»κ![]() ΒΟ
ΒΟ![]()
![]() –ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣ
–ΓΆθΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ
Ζ÷÷”Θ§–Γ’≈ΒΡ ΒΦ ––≥Β ±ΦδΈΣ![]() Ζ÷÷”Θ°
Ζ÷÷”Θ°


 » Α°”Δ”οΆ§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ
» Α°”Δ”οΆ§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ ―ßœΑ ΒΦυ‘ΑΒΊœΒΝ–¥πΑΗ
―ßœΑ ΒΦυ‘ΑΒΊœΒΝ–¥πΑΗ
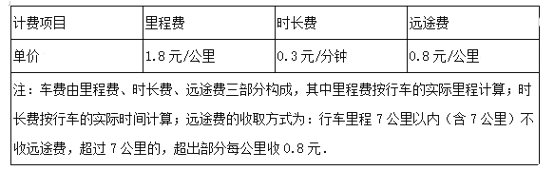
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν– ¬Φΰ τ”Ύ±Ί»Μ ¬ΦΰΒΡ «Θ®ΓΓΓΓΘ©
A. ¥ρΩΣΒγ ”Θ§’ΐ‘Ύ≤Ξ≥ωœΒΝ–Ή®ΧβΤ§ΓΑΚΫ≈Ρ÷–ΙζΓ±
B. »τ‘≠ΟϋΧβ≥…ΝΔΘ§‘ρΥϋΒΡΡφΟϋΧβ“ΜΕ®≥…ΝΔ
C. “ΜΉι ΐΨίΒΡΖΫ≤ν‘Ϋ–ΓΘ§‘ρ’βΉι ΐΨίΒΡ≤®Ε·‘Ϋ–Γ
D. ‘Ύ ΐ÷α…œ»Έ»Γ“ΜΒψΘ§‘ρΗΟΒψ±μ ΨΒΡ ΐ“ΜΕ® «”–άμ ΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΨΊ–ΈABCDΒΡ±ΏABΘΫ4Θ§BCΘΫ6Θ°»τ≤ΜΗΡ±δΨΊ–ΈABCDΒΡ–ΈΉ¥ΚΆ¥σ–ΓΘ§Β±ΨΊ–ΈΕΞΒψA‘Ύx÷αΒΡ’ΐΑκ÷α…œΉσ”““ΤΕ· ±Θ§ΨΊ–ΈΒΡΝμ“ΜΗωΕΞΒψD Φ÷’‘Ύy÷αΒΡ’ΐΑκ÷α…œΥφ÷°…œœ¬“ΤΕ·Θ°
(1)Β±ΓœOADΘΫ30Γψ ±Θ§«σΒψCΒΡΉχ±ξΘΜ
(2)…ηADΒΡ÷–ΒψΈΣMΘ§Ν§Ϋ”OMΓΔMCΘ§Β±ΥΡ±Ώ–ΈOMCDΒΡΟφΜΐΈΣ![]() ±Θ§«σOAΒΡ≥ΛΘΜ
±Θ§«σOAΒΡ≥ΛΘΜ
(3)Β±ΒψA“ΤΕ·ΒΫΡ≥“ΜΈΜ÷Ο ±Θ§ΒψCΒΫΒψOΒΡΨύάκ”–Ήν¥σ÷ΒΘ§«κ÷±Ϋ”–¥≥ωΉν¥σ÷ΒΘ§≤Δ«σ¥Υ ±cosΓœOADΒΡ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬±μ «ΦΉΓΔ““ΝΫΟϊΆ§―ßΫϋΈε¥Έ ΐ―ß≤β ‘Θ®¬ζΖ÷ΨυΈΣ100Ζ÷Θ©ΒΡ≥…Φ®Ά≥ΦΤ±μΘΚ
Ά§―ß | ΒΎ“Μ¥Έ | ΒΎΕΰ¥Έ | ΒΎ»ΐ¥Έ | ΒΎΥΡ¥Έ | ΒΎΈε¥Έ |
ΦΉ | 90 | 88 | 92 | 94 | 91 |
““ | 90 | 91 | 93 | 94 | 92 |
ΗυΨί…œ±μ ΐΨίΘ§≥…Φ®ΫœΚΟ«“±»ΫœΈ»Ε®ΒΡΆ§―ß «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
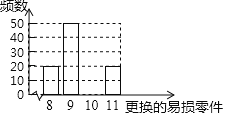
ΓΨΧβΡΩΓΩΡ≥÷÷ΜζΤς Ι”Ο»τΗ…ΡξΚσΦ¥±ΜΧ‘Χ≠Θ§ΗΟΜζΤς”–“Μ“ΉΥπΝψΦΰΘ§ΈΣΒς≤ιΗΟ“ΉΥπΝψΦΰΒΡ Ι”Ο«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ100Χ®“―±ΜΧ‘Χ≠ΒΡ’β÷÷ΜζΤςΘ§Ψ≠Ά≥ΦΤΘΚΟΩΧ®ΜζΤς‘Ύ Ι”ΟΤΎΡΎΗϋΜΜΒΡΗΟ“ΉΥπΝψΦΰ ΐΨυ÷Μ”–8Θ§9Θ§10Θ§11’βΥΡ÷÷«ιΩωΘ§≤Δ’ϊάμΝΥ’β100Χ®ΜζΤς‘Ύ Ι”ΟΤΎΡΎΗϋΜΜΒΡΗΟ“ΉΥπΝψΦΰ ΐΘ§Μφ÷Τ≥…»γΆΦΥυ Ψ≤ΜΆξ’ϊΒΡΧθ–ΈΆ≥ΦΤΆΦΘ°
Θ®1Θ©«κ≤Ι»ΪΗΟΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©Ρ≥ΙΪΥΨΦΤΜ°ΙΚ¬ρ“ΜΧ®’β÷÷ΜζΤς“‘ΦΑ»τΗ…ΗωΗΟ“ΉΥπΝψΦΰΘ§”Ο…œ ω100Χ®ΜζΤςΗϋΜΜΒΡΗΟ“ΉΥπΝψΦΰ ΐΒΡΤΒ¬ ¥ζΧφ“ΜΧ®ΜζΤςΗϋΜΜΒΡΗΟ“ΉΥπΝψΦΰ ΐΖΔ…ζΒΡΗ≈¬ Θ°
ΔΌ«σ’βΧ®ΜζΤς‘Ύ Ι”ΟΤΎΡΎΙ≤ΗϋΜΜΝΥ9ΗωΗΟ“ΉΥπΝψΦΰΒΡΗ≈¬ ΘΜ
ΔΎ»τ‘ΎΙΚ¬ρΜζΤςΒΡΆ§ ±ΙΚ¬ρΗΟ“ΉΥπΝψΦΰΘ§‘ρΟΩΗω200‘ΣΘΜ»τ‘Ύ Ι”ΟΙΐ≥Χ÷–Θ§“ρ±Η”ΟΗΟ“ΉΥπΝψΦΰ≤ΜΉψΘ§‘ΌΙΚ¬ρΘ§‘ρΟΩΗω500‘ΣΘ°«κΡψΑοΗΟΙΪΥΨ”ΟΜ®‘ΎΗΟ“ΉΥπΝψΦΰ…œΒΡΖ―”ΟΒΡΦ”»®ΤΫΨυ ΐΫχ––Ψω≤ΏΘΚΙΚ¬ρΜζΤςΒΡΆ§ ±”ΠΙΚ¬ρΦΗΗωΗΟ“ΉΥπΝψΦΰΘ§Ω… ΙΙΪΥΨΒΡΜ®Ζ―Ήν…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
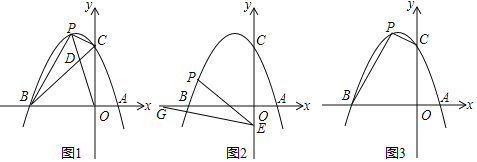
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏyΘΫax2+bx+3Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆΒψBΘ®©¹3Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψPΈΣΒΎΕΰœσœόΡΎ≈ΉΈοœΏ…œΒΡΕ·Βψ.
Θ®1Θ©≈ΉΈοœΏΒΡΫβΈω ΫΈΣ Θ§≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣ ΘΜ
Θ®2Θ©»γΆΦ1Θ§Ν§Ϋ”OPΫΜBC”ΎΒψDΘ§Β±SΓςCPDΘΚSΓςBPDΘΫ1ΘΚ2 ±Θ§«κ«σ≥ωΒψDΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§ΒψEΒΡΉχ±ξΈΣΘ®0Θ§©¹1Θ©Θ§ΒψGΈΣx÷αΗΚΑκ÷α…œΒΡ“ΜΒψΘ§ΓœOGEΘΫ15ΓψΘ§Ν§Ϋ”PEΘ§»τΓœPEGΘΫ2ΓœOGEΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ
Θ®4Θ©»γΆΦ3Θ§ «Ζώ¥φ‘ΎΒψPΘ§ ΙΥΡ±Ώ–ΈBOCPΒΡΟφΜΐΈΣ8ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§BC «Γ―OΒΡœ“Θ§÷±œΏMN”κΓ―Oœύ«–”ΎΒψCΘ§ΙΐΒψBΉςBDΓΆMN”ΎΒψDΘ°
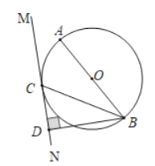
Θ®1Θ©«σ÷ΛΘΚΓœABCΘΫΓœCBDΘΜΘ®2Θ©»τBCΘΫ4![]() Θ§CDΘΫ4Θ§‘ρΓ―OΒΡΑκΨΕ «ΓΓ ΓΓΘ°
Θ§CDΘΫ4Θ§‘ρΓ―OΒΡΑκΨΕ «ΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓ―OΒΡ÷±ΨΕCD¥Ι÷±”Ύœ“ABΘ§¥ΙΉψΈΣΒψEΘ§ΓœACD=22.5ΓψΘ§»τCD=6cmΘ§‘ρABΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©
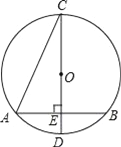
A. 4cm B. 3![]() cm C. 2
cm C. 2![]() cm D. 2
cm D. 2![]() cm
cm
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ≥ΒΖ÷±π¥”![]() ΝΫΒΊΆ§ ±≥ωΖΔΘ§―ΊΆ§“ΜΧθΙΪ¬Ζœύœρ–– ΜΘ§œύ”ωΚσΘ§ΦΉ≥ΒΦΧ–χ“‘‘≠ΥΌ–– ΜΒΫ
ΝΫΒΊΆ§ ±≥ωΖΔΘ§―ΊΆ§“ΜΧθΙΪ¬Ζœύœρ–– ΜΘ§œύ”ωΚσΘ§ΦΉ≥ΒΦΧ–χ“‘‘≠ΥΌ–– ΜΒΫ![]() ΒΊΘ§““≥ΒΝΔΦ¥“‘‘≠ΥΌ‘≠¬ΖΖΒΜΊΒΫ
ΒΊΘ§““≥ΒΝΔΦ¥“‘‘≠ΥΌ‘≠¬ΖΖΒΜΊΒΫ![]() ΒΊΘ§ΦΉΓΔ““ΝΫ≥ΒΨύ
ΒΊΘ§ΦΉΓΔ““ΝΫ≥ΒΨύ![]() ΒΊΒΡ¬Ζ≥Χ
ΒΊΒΡ¬Ζ≥Χ![]() ”κΗςΉ‘–– ΜΒΡ ±Φδ
”κΗςΉ‘–– ΜΒΡ ±Φδ![]() ÷°ΦδΒΡΙΊœΒ»γΆΦΥυ ΨΘ°
÷°ΦδΒΡΙΊœΒ»γΆΦΥυ ΨΘ°
Δ≈![]() ________Θ§
________Θ§![]() ________ΘΜ
________ΘΜ
ΔΤ«σ““≥ΒΨύ![]() ΒΊΒΡ¬Ζ≥Χ
ΒΊΒΡ¬Ζ≥Χ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩ
ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Δ«Β±ΦΉ≥ΒΒΫ¥ο![]() ΒΊ ±Θ§«σ““≥ΒΨύ
ΒΊ ±Θ§«σ““≥ΒΨύ![]() ΒΊΒΡ¬Ζ≥Χ
ΒΊΒΡ¬Ζ≥Χ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
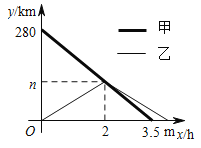
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com