
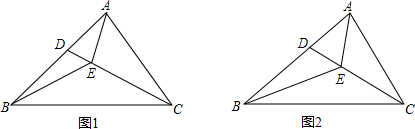
分析 (1)由等腰三角形的性质得到∠EBC=∠ECB=27°,根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°,再由角平分线的性质得到∠ACD=∠ECB=27°,因为∠EAC=2∠EBC=54°,求得∠AEC=180°-27°-54°=99°;
(2)①在BC上取一点M,使BM=ME,根据等腰三角形的性质得到∠MBE=∠MEB,由∠EAB=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,得到∠EAC=∠EMC,由全等三角形的性质推出AE=ME,CM=AC,于是得到结论;
②如图2,在BC上取一点M,使BM=ME,连接AM,由∠ECB=30°,得到∠ACB=60°,于是推出△AMC是等边三角形,通过三角形全等得到∠EBC=∠MAE,由∠MAC=60°,得到∠EAC=2∠EBC=2∠MAE,于是得出结果.
解答 解:(1)∵EB=EC,
∴∠EBC=∠ECB=27°,
∵CD平分∠ACB,
∴∠ACD=∠ECB=27°,
∵∠EAC=2∠EBC=54°,
∴∠AEC=180°-27°-54°=99°,
故答案为:27°,99°;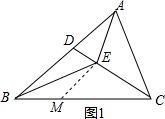
(2)①证明:如图1,在BC上取一点M,使BM=ME,
∴∠MBE=∠MEB,
∵∠EAC=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,
∴∠EAC=∠EMC,
在△ACE与△MCE中,
$\left\{\begin{array}{l}{∠CAE=∠CME}\\{∠ACE=∠MCE}\\{CE=CE}\end{array}\right.$,
∴△ACE≌△MCE,
∴AE=ME,CM=AC,
∴AE=BM,
∴BC=BM+CM=AE+AC;
②如图2在BC上取一点M,使BM=ME,连接AM,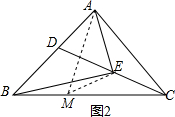
∵∠ECB=30°,
∴∠ACB=60°,由①可知;△AMC是等边三角形(M点与B点重合),
∴AM=AC=BE,
在△EMB与△MEA中,
$\left\{\begin{array}{l}{AE=BM}\\{EM=EM}\\{AM=BE}\end{array}\right.$,
∴∠EBC=∠MAE,
∵∠MAC=60°,
∵∠EAC=2∠EBC=2∠MAE,
∴∠MAE=20°,∠EAC=40°,
∴∠EBC=20°.
点评 本题考查了全等三角形的判定与性质,角平分线的性质,等边三角形的性质,外角的性质,正确的作出辅助线是解题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
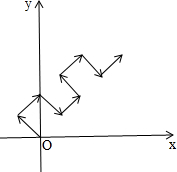 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )| A. | (9,11) | B. | (11,11) | C. | (10,10) | D. | (10,12) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
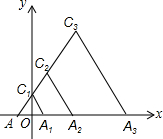 如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0).
如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com