
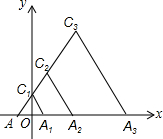
 如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0).
如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0). 分析 由图可知:纵坐标都为0,点A1的横坐标为0.5,点A2的横坐标为0.5+1=1.5=2-0.5,点A3的横坐标为0.5+1+2=3.5=4-0.5,点A4的横坐标为0.5+1+2+4=7.5=8-0.5,…由此得出点An的横坐标为2n-1-0.5,解决问题.
解答 解:∵点A1的横坐标为0.5=1-0.5,
点A2的横坐标为0.5+1=1.5=2-0.5,
点A3的横坐标为0.5+1+2=3.5=4-0.5,
点A4的横坐标为0.5+1+2+4=7.5=8-0.5,
…
∴点An的横坐标为2n-1-0.5,纵坐标都为0,
∴点An的坐标为(2n-1-0.5,0).
故答案为:(2n-1-0.5,0).
点评 此题考查点的坐标规律,等边三角形的性质,找出点的横坐标变化的规律是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
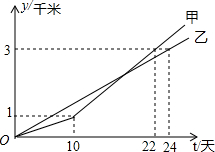 某工程队承包了一段道路修建工程,为了加快修建速度,工程负责人将工程队分为甲乙两组,从路的两端同时开工,两个组修建道路的长度y千米)与施工时间t(天)的关系如图所示.
某工程队承包了一段道路修建工程,为了加快修建速度,工程负责人将工程队分为甲乙两组,从路的两端同时开工,两个组修建道路的长度y千米)与施工时间t(天)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
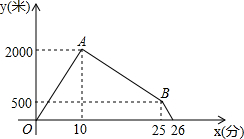 琪琪周日早晨8:00之前要赶到距家8000米的烈士陵园去扫墓,她早上7:20出发,10分钟后父亲发现她忘了带演讲稿,于是立即出发,按琪琪走得路线去追,父亲出发几分钟后,琪琪也发现忘记了带演讲稿,于是立即原路返回去取,1分钟后与父亲相遇,然后父亲立即返回,琪琪赶往陵园.已知父女二人速度始终不变,如图给出了两人之间的距离S(米)和琪琪行驶时间t (分)之间的函数图象.
琪琪周日早晨8:00之前要赶到距家8000米的烈士陵园去扫墓,她早上7:20出发,10分钟后父亲发现她忘了带演讲稿,于是立即出发,按琪琪走得路线去追,父亲出发几分钟后,琪琪也发现忘记了带演讲稿,于是立即原路返回去取,1分钟后与父亲相遇,然后父亲立即返回,琪琪赶往陵园.已知父女二人速度始终不变,如图给出了两人之间的距离S(米)和琪琪行驶时间t (分)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{n}{t-0.5}$ | B. | $\frac{n}{t}$ | C. | $\frac{n}{t-0.5}$-$\frac{n}{t}$ | D. | $\frac{n}{t}$-$\frac{n}{t-0.5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
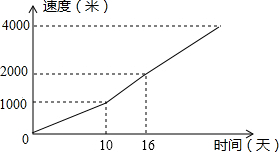 为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示:
为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com