
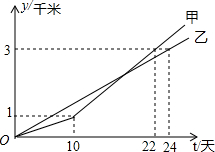
 某工程队承包了一段道路修建工程,为了加快修建速度,工程负责人将工程队分为甲乙两组,从路的两端同时开工,两个组修建道路的长度y千米)与施工时间t(天)的关系如图所示.
某工程队承包了一段道路修建工程,为了加快修建速度,工程负责人将工程队分为甲乙两组,从路的两端同时开工,两个组修建道路的长度y千米)与施工时间t(天)的关系如图所示.分析 (1)根据图象分析,甲组开工10天后修路长度y1与t的函数图象是过点(10,1)与点(22,3)的直线,用待定系数法,设解析式为y1=k1t+b,代入可得结果,乙组修路长度y2与t的函数图象是过点(0,0)与点(24,3)的直线,设解析式为y1=k2t,代入可得结果;
(2)两个组修建道路长度相同,即y相同,根据解析式建立等式可得t.
解答 解:(1)由图象可知,y1与t的函数图象是过点(10,1)与点(22,3)的直线,
设其解析式为:y1=k1t+b,
将(10,1)与(22,3)代入得:
$\left\{\begin{array}{l}{1=1{0k}_{1}+b}\\{3=2{2k}_{1}+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{6}}\\{b=-\frac{2}{3}}\end{array}\right.$,
∴y1与t的函数关系式为:${y}_{1}=\frac{1}{6}t-\frac{2}{3}$,
由图象可知,y2与t的函数图象是过点(0,0)与点(24,3)的直线,
设y2与t的解析式为:y2=k2t,
将(24,3)代入得:
3=24k2,解得:k2=$\frac{1}{8}$,
∴y2与t的函数关系式为:y2=$\frac{1}{8}$t;
(2)由题意得:当y1=y2时,两个组修建道路长度相同.,∴$\frac{1}{6}t-\frac{2}{3}$=$\frac{1}{8}$t,解得:t=16,
∴开工16天后,两个组修建道路长度相同.
点评 本题主要考查的是用一次函数解决实际问题,数形结合,能够根据题意中的等量关系建立函数关系式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
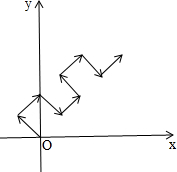 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )| A. | (9,11) | B. | (11,11) | C. | (10,10) | D. | (10,12) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
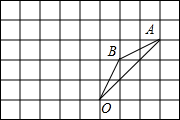 如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
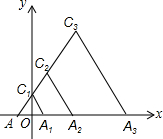 如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0).
如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3,…,按此规律继续画等边三角形,则点An的坐标为(2n-1-0.5,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 883.6×108 | B. | 8.836×108 | C. | 8.836×109 | D. | 8.836×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某高校共有5个一样规模的大餐厅和3个一样规模的小餐厅.经过测试:同时开放3个大餐厅、2个小餐厅,可供3300名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2100名学生就餐.
某高校共有5个一样规模的大餐厅和3个一样规模的小餐厅.经过测试:同时开放3个大餐厅、2个小餐厅,可供3300名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2100名学生就餐.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com