
【题目】启明公司生产某种产品,每件成本是3元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x( 万元)时,产品的年销售量是原销售量的y倍,且y=![]() . 如果把利润看作是销售总额减去成本和广告费:
. 如果把利润看作是销售总额减去成本和广告费:
(1)试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?
(2)把(1)中的最大利润留出3万元做广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:
项目 | A | B | C | D | E | F |
每股(万元) | 5 | 2 | 6 | 4 | 6 | 8 |
收益(万元) | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 1 |
如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元, 问有几种符合要求的方式?写出每种投资方式所选的项目.
【答案】(1)s=-x2+6x+7,当广告费是3万元时,公司获得的最大年利润是16万元.
(2)有下列两种投资方式符合要求:①取A、B、E各一股,②取B、D、E各一股
【解析】
试题(1)根据年利润=单利润×年销售量即可得到函数关系式,再根据二次函数的性质即可得到结果;
(2)根据广告3万元,投资项目的收益总额不低于1.6万元,再仔细分析表中数据即可得到结果.
(1)s=10×![]() ×(4-3)-x=-x2+6x+7.
×(4-3)-x=-x2+6x+7.
当x=![]() =3 时,
=3 时,
S最大=![]() =16.
=16.
∴当广告费是3万元时,公司获得的最大年利润是16万元.
(2)用于再投资的资金有=16-3=13万元.
有下列两种投资方式符合要求:
①取A、B、E各一股,投入资金为5+2+6=13万元,
收益为0.55+0.4+0.9=1.85万元>1.6万元.
②取B、D、E各一股,投入资金为2+4+6=12万元<13万元,
收益为0.4+0.5+0.9=1.8万元>1.6万元 .


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③△ABD是等腰三角形
④点D到直线AB的距离等于CD的长度.
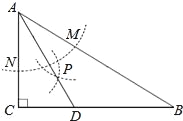
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(高成都绩于50分),绘制了如下的统计图表(不完整);

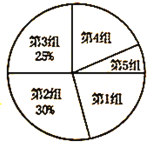
请根据以上信息,解答下列问题:
(1)求出![]() 、
、![]() 的值;
的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个等腰Rt△ADE、Rt△ABC如图放置在一起,其中∠DAE=∠ABC=90°.点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ;正确的个数是( )
;正确的个数是( )
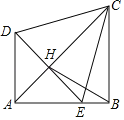
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
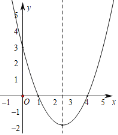
(1)求该抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速铁路位于某省南部,是国家“八纵八横”高速铁路网的重要连接通道,也是某省“三横五纵”高速铁路网的重要组成部分.东起日照,向西贯穿临沂、曲阜、济宁、菏泽,与郑徐客运专线兰考南站接轨.工程有一段在一条河边,且刚好为东西走向.B处是一个高铁维护站,如图①,现在想过B处在河上修一座桥,需要知道河宽,一测量员在河对岸的A处测得B在它的东北方向,测量员从A点开始沿岸边向正东方向前进300米到达点C处,测得B在C的北偏西30度方向上.
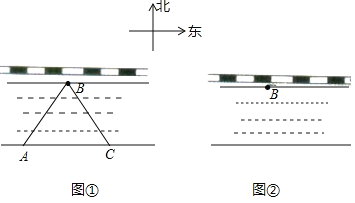
(1)求所测之处河的宽度;(结果保留的十分位)
(2)除(1)的测量方案外,请你再设计一种测量河宽的方案,并在图②中画出图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
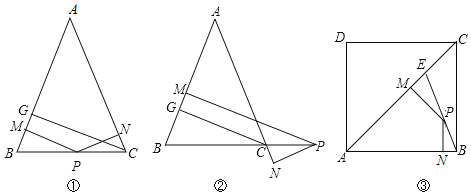
【题目】如图①,已知△ABC中,AB=AC,点P是BC上的一点,PN⊥AC于点N,PM⊥AB于点M,CG⊥AB于点G点.
(1)则线段CG、PM、PN三者之间的数量关系是 ;
(2)如图②,若点P在BC的延长线上,则线段CG、PM、PN三者是否还有上述关系,若有,请说明理由,若没有,猜想三者之间又有怎样的关系,并证明你的猜想;
(3)如图③,点E在正方形ABCD的对角线AC上,且AE=AD,点P是BE上任一点,PN⊥AB于点N,PM⊥AC于点M,若正方形ABCD的面积是12,请直接写出PM+PN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
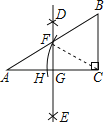
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com