
【题目】将两个等腰Rt△ADE、Rt△ABC如图放置在一起,其中∠DAE=∠ABC=90°.点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ;正确的个数是( )
;正确的个数是( )
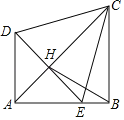
A.1B.2C.3D.4
【答案】D
【解析】
利用等腰直角三角形的性质得出∠DAC=∠BAC即可判断出①正确;再用等腰直角三角形的内角的关系即可得出∠DCE=60°,即可得出②正确,判断出∠BCD=75°=∠BEC即可判断出③正确,设出AH=x,利用等腰直角三角形和等边三角形的性质即可得出CH,EH,AB,BE最后用三角形的面积公式即可得出④正确.
解:∵△ABC和△ADE是等腰直角三角形,
∴∠BAC=∠ACB=45°,∠DAE=90°,
∴∠DAC=∠BAC=45°,
∵AD=AE,
∴AC垂直平分DE,∴①正确,
∵AC垂直平分DE,
∴DC=EC,∠DAC=∠EAC,
∵∠BCE=15°,
∴∠ACE=30°,
∴∠DCE=2∠ACE=60°,
∴△CDE是等边三角形,∴②正确;
∵∠DCE=60°,∠BCE=15°,
∴∠BCD=75°,
∵∠BEC=90°﹣15°=75°,
∴∠BCD=∠BEC,
在Rt△BCE中,![]() ,
,
∴tan∠BCD=![]() ,故③正确;
,故③正确;
设AH=x,
在Rt△AEH中,HE=AH=x,AE=![]() x,
x,
在Rt△CEH中,∠ECH=30°,
∴CH=![]() EH=
EH=![]() x,CE=2HE=2x,
x,CE=2HE=2x,
∴AC=AH+CH=(![]() +1)x,
+1)x,
在Rt△ABC中,![]() ,
,
∴BE=AB﹣AE![]() ,
,
![]() ,
,
![]() ,
,
![]() .故④正确,
.故④正确,
故选:D.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了取得扶贫工作的胜利,某市对扶贫工作人员进行了扶贫知识的培训与测试,随机抽取了部分人员的测试成绩作为样本,并将成绩划分为![]() 四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
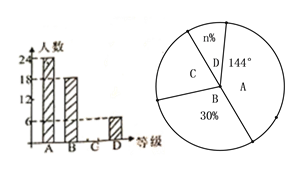
(1)求样本容量;
(2)补全条形图,并填空: ![]() ;
;
(3)若全市有5000人参加了本次测试,估计本次测试成绩为![]() 级的人数为多少?
级的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的最高点的纵坐标是2.
的最高点的纵坐标是2.
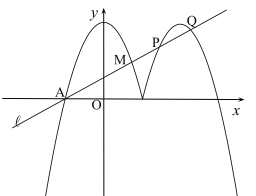
(1)求抛物线的表达式;
(2)将抛物线在![]() 之间的部分记为图象
之间的部分记为图象![]() ,将图象
,将图象![]() 沿直线x=1翻折,翻折后图象记为
沿直线x=1翻折,翻折后图象记为![]() ,图象
,图象![]() 和
和![]() 组成G,直线
组成G,直线![]() :
:![]()
![]() 和图象G在x轴上方的部分有两个公共点,求k的取值范围;
和图象G在x轴上方的部分有两个公共点,求k的取值范围;
(3)直线![]() :
:![]() 与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求
与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接一铁路工程,在挖掘一条500米长的隧道时,为了尽快完成,实际施工时每天挖掘的长度是原计划的1.5倍,结果提前了25天完成了其中300米的隧道挖掘任务.
(1)求实际每天挖掘多少米?
(2)由于气候等原因,需要进一步缩短工期,要求完成整条隧道不超过70天,那么为了完成剩下的任务,在实际每天挖掘长度的基础上,至少每天还应多挖掘多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=![]() (x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
(x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
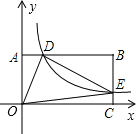
查看答案和解析>>
科目:初中数学 来源: 题型:
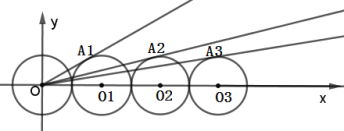
【题目】如图,在平面直角坐标中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 的圆心在
的圆心在![]() 轴上,且半径均为
轴上,且半径均为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]()
![]()
![]() 射线
射线![]() 与
与![]() 相切于点
相切于点![]() ,射线
,射线![]() 与
与![]() 相切于点
相切于点![]() ,按照这样的规律,
,按照这样的规律,![]() 的横坐标为_____.
的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
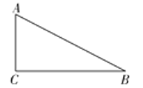
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用尺规作图法,作∠ACB的平分线CD,交AB于点D;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,过点D分别作 DE⊥AC于点E,DF⊥BC于点F.求证:四边形CEDF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com