
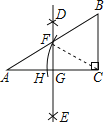
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
科目:初中数学 来源: 题型:
【题目】启明公司生产某种产品,每件成本是3元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x( 万元)时,产品的年销售量是原销售量的y倍,且y=![]() . 如果把利润看作是销售总额减去成本和广告费:
. 如果把利润看作是销售总额减去成本和广告费:
(1)试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?
(2)把(1)中的最大利润留出3万元做广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:
项目 | A | B | C | D | E | F |
每股(万元) | 5 | 2 | 6 | 4 | 6 | 8 |
收益(万元) | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 1 |
如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元, 问有几种符合要求的方式?写出每种投资方式所选的项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有两点![]() 、
、![]() ,若满足:当
,若满足:当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,则称点为点的“友好点”.
,则称点为点的“友好点”.
(1)点![]() 的“友好点”的坐标是_______.
的“友好点”的坐标是_______.
(2)点![]() 是直线
是直线![]() 上的一点,点
上的一点,点![]() 是点
是点![]() 的“友好点”.
的“友好点”.
①当![]() 点与
点与![]() 点重合时,求点
点重合时,求点![]() 的坐标.
的坐标.
②当![]() 点与
点与![]() 点不重合时,求线段
点不重合时,求线段![]() 的长度随着
的长度随着![]() 的增大而减小时,
的增大而减小时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆上一个动点(不与点A,B重合),D是弦AC上一点,过点D作DE⊥AB,垂足为E,过点C作半圆O的切线,交ED的延长线于点F.
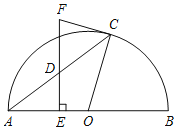
(1)求证:FC=FD.
(2)①当∠CAB的度数为 时,四边形OEFC是矩形;②若D是弦AC的中点,⊙O的半径为5,AC=8,则FC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径作⊙O、交AB于点D,E为AC的中点,连接DE
(1)求证:DE为⊙O的切线;
(2)已知BC=4.填空.
①当DE= 时,四边形DOCE为正方形;
②当DE= 时,△BOD为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
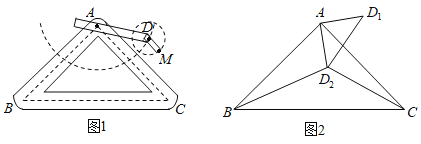
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠B=60°,AB=6,BC=12.点E是BC上一动点,将△ABE沿直线AE折叠,得到△AFE,则当AF与ABCD的边垂直时,BE的长为_____.
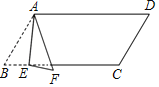
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com