
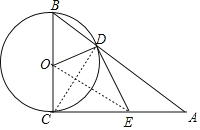
【题目】如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径作⊙O、交AB于点D,E为AC的中点,连接DE
(1)求证:DE为⊙O的切线;
(2)已知BC=4.填空.
①当DE= 时,四边形DOCE为正方形;
②当DE= 时,△BOD为等边三角形.

【答案】(1)证明见解析;(2)①2;②2![]() .
.
【解析】
(1)连接CD,根据圆周角定理得出∠CDB=90°,根据直角三角形性质得出DE=CE=AE,求出∠ACD+∠DCO=∠EDC+∠CDO,求出OD⊥DE,根据切线的判定得出即可;
(2)①若四边形DOCE为正方形,则OC=OD=DE=CE=2;
②若△BOD为等边三角形,则∠DOE=60°,则Rt△ODE中,则DE=2![]() .
.
(1)如图,连接CD,OE,
∵BC为⊙O的直径,
∴∠BDC=90°,
∵DE为Rt△ADC的斜边AC上的中线,
在△COE与△DOE中,OD=CC,OE=OE,DE=CE,
∴△COE≌△DOE,
∴∠OCE=∠ODE=90°,
DE为⊙O的切线;
(2)①若四边形DOCE为正方形,则OC=OD=DE=CE,
∵BC=4,
∴DE=2.
②若△BOD为等边三角形,
∴∠BOD=60°,
∴∠COD=180°﹣∠BOD=120°,
∴∠DOE=60°,
∴Rt△ODE中,DE=OD![]() .
.
故答案为:2,2![]() .
.


科目:初中数学 来源: 题型:
【题目】某高速铁路位于某省南部,是国家“八纵八横”高速铁路网的重要连接通道,也是某省“三横五纵”高速铁路网的重要组成部分.东起日照,向西贯穿临沂、曲阜、济宁、菏泽,与郑徐客运专线兰考南站接轨.工程有一段在一条河边,且刚好为东西走向.B处是一个高铁维护站,如图①,现在想过B处在河上修一座桥,需要知道河宽,一测量员在河对岸的A处测得B在它的东北方向,测量员从A点开始沿岸边向正东方向前进300米到达点C处,测得B在C的北偏西30度方向上.
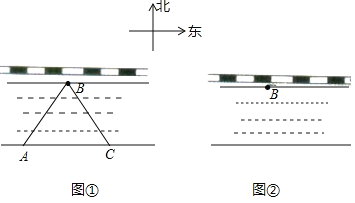
(1)求所测之处河的宽度;(结果保留的十分位)
(2)除(1)的测量方案外,请你再设计一种测量河宽的方案,并在图②中画出图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
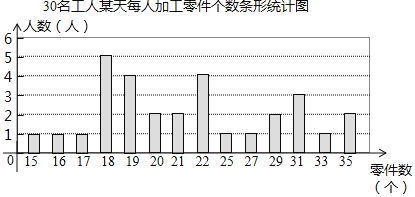
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
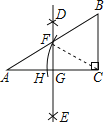
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
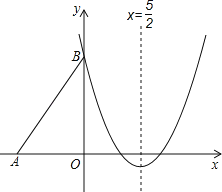
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=![]() x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x=![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
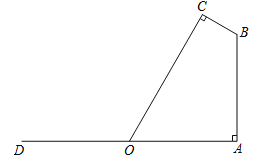
【题目】如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+6x﹣5与x轴交于A,B两点(点A在点B左边),与y轴交于点C.点P是抛物线上一个动点,过点P作x轴的垂线,垂足为点H,交直线BC于点E.
(1)求点A,B,C的坐标;
(2)连接CP,当CP平分∠OCB时,求点P的坐标;
(3)平面直角坐标系内是否存在点Q,使得以点P,E,B,Q为顶点的四边形为菱形?若存在,直接写出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com