
分析 需要对a的取值范围进行分类讨论:a>10、2<a<10、a<2.根据a的取值范围得到不同的方程,结合根的判别式来解答.
解答 解:①当a>10时,方程可化为:(a+1)x2+12x+a-5=0,
△=122-4(a+1)(a-5)>0,
解得a<6.2.不合题意;
②当2<a<10时,方程可化为:(a+1)x2+(2a-8)x+5=0,
△=(2a-8)2-20(a+1)>0,即a2-13a+11>0.
解得a>$\frac{13+5\sqrt{5}}{2}$或a<$\frac{13-5\sqrt{5}}{2}$.
所以a的取值范围是:2<a<10.
③当a<2时,方程可化为:(a+1)x2-12x+5=0,
△=144-20(a+1)>0,
解得a<6.2.
综上所述,a的取值范围为:2<a<10.
故答案是:2<a<10.
点评 本题考查了根的判别式.解题时,要对a的取值范围进行分类讨论,以防漏解或错解.


科目:初中数学 来源: 题型:解答题
 如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
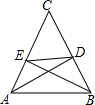 已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )
已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )| A. | $\sqrt{2}$:2 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
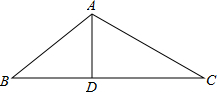 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com