
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点A、C的坐标分别为(-4,3)、(-1,1).
的顶点A、C的坐标分别为(-4,3)、(-1,1).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出![]() 关于y对称的△A′B′C′;
关于y对称的△A′B′C′;
(3)写出点![]() 的坐标 ;
的坐标 ;![]() 的面积为 .
的面积为 .
(4)若在y轴上有点M,则能使△ABM的周长最小的点M的坐标为 .

【答案】(1)见解析;(2)见解析;(3)(2,-1),4;(4)(0,![]() ).
).
【解析】
(1)根据A、C两点的坐标建立直角坐标系即可;
(2)分别作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B′在坐标系中的位置写出其坐标,利用割补法进行计算,即可得![]() 的面积;
的面积;
(4)利用待定系数法求出直线AB′的解析式,进而可得出在y轴上能使△ABM的周长最小的点M的坐标.
解:(1)坐标系如图;

(2)如图,△A′B′C′即为所求;
(3)由图可知,B′(2,-1),
S△ABC=3×4-![]() ×2×4-
×2×4-![]() ×2×3-
×2×3-![]() ×1×2
×1×2
=12-4-3-1
=4;
(4)如图所示,点M即为所求点,
设直线AB′的解析式为y=kx+b(k≠0),
∵(-4,3),B′(2,-1),
∴![]() ,解得
,解得 ,
,
∴直线AB′的解析式为![]() .
.
∵当x=0时,y=![]() ,
,
∴M(0,![]() ).
).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.

(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

查看答案和解析>>
科目:初中数学 来源: 题型:
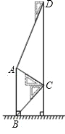
【题目】如图,某中学在教学楼前新建了一座雕塑![]() .为了测量雕塑的高度,小明在二楼找到一点
.为了测量雕塑的高度,小明在二楼找到一点![]() ,利用三角尺测得雕塑顶端点
,利用三角尺测得雕塑顶端点![]() 的仰角为
的仰角为![]() ,底部点
,底部点![]() 的俯角为
的俯角为![]() ,小华在五楼找到一点
,小华在五楼找到一点![]() ,利用三角尺测得点
,利用三角尺测得点![]() 的俯角为
的俯角为![]() .若
.若![]() 为
为![]() ,则雕塑
,则雕塑![]() 的高度为________
的高度为________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-![]() x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.

(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m﹣n)2=0,(n﹣4)2=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴n=4,m=4.
∴(m﹣n)2+(n﹣4)2=0,
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
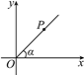
【题目】如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的夹角为α,则用[ρ,α]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[![]() ,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
A. (-2,2![]() ) B. (2,-2
) B. (2,-2![]() ) C. (-2
) C. (-2![]() ,-2) D. (-4,-4
,-2) D. (-4,-4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
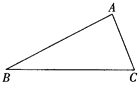
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D,当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC此时BE与DC有怎样的位置关系?________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com