
【题目】某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.
厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数,2、结合转盘简述获奖方式,不需说明理由.)
【答案】(1)该抽奖方案符合厂家的设奖要求,理由详见解析;(2)详见解析.
【解析】
(1)列出所有情况,看摸到的2个球都是黄球的情况占所有情况的多少即可求得获大奖的概率,进而求得获小奖的概率 (2)让表示大奖的角的度数占圆周角的0.1倍即可
(1)该抽奖方案符合厂家的设奖要求:
分别用黄1、黄2、白1、白2、白3表示这5个球,从中任意摸出2个球,可能出现的结果有:
(黄1,黄2)、(黄1,白1)、(黄1,白2)、(黄1,白3)、
(黄2,黄1)、(黄2,白1)、(黄2,白2)、(黄2,白3)、
(白1,黄1)、(白1,黄2)、(白1.白2)、(白1,白3)、
(白2,黄1)、(白2,黄2)、(白2,白1)、(白2,白3)、
(白3,黄1)、(白3,黄2)、(白3,白1)、(白3,白2)
共有20种,它们出现的可能性相同.
所有的结果中,满足摸到的2个球都是黄球(记为事件A)的结果有2种,即(黄1,黄2)或(黄2,黄1),
所以P(两黄球)=![]() =
=![]() ,即顾客获得大奖的概率为10%,获得小奖的概率为90%;
,即顾客获得大奖的概率为10%,获得小奖的概率为90%;
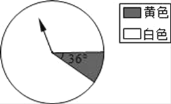
(2)本题答案不唯一,下列解法供参考.
如图,将转盘中圆心角为36°的扇形区域涂上黄色,其余的区域涂上白色,顾客每购买一台该型号电视机,可获得一次转动转盘的机会,任意转动这个转盘,当转盘停止时,指针指向黄色区域获得大奖,指向白色区域获得小奖.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc<0;②4a+2b+c>0;③b2-4ac<0;④b>a+c;⑤a+2b+c>0,其中正确的结论有( )
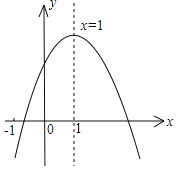
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
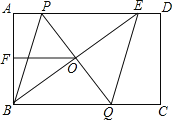
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:△BOQ≌△EOP;
(2)求证:四边形BPEQ是菱形;
(3)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
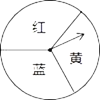
A. 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B. 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C. 掷一枚质地均匀的骰子,奇数点朝上代表正面,偶数点朝上代表反面
D. 转动如图所示的转盘,指针指向“红”代表正面,指针指向“蓝”代表反面
查看答案和解析>>
科目:初中数学 来源: 题型:
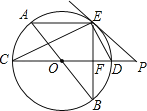
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E。那么点D的坐标为( )
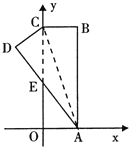
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
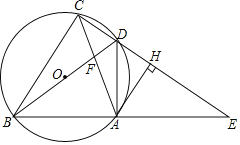
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com