
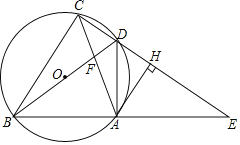
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)连接OA,证明△DAB≌△DAE,得到AB=AE,得到OA是△BDE的中位线,根据三角形中位线定理、切线的判定定理证明;
(2)利用正弦的定义计算;
(3)证明△CDF∽△AOF,根据相似三角形的性质得到CD=![]() CE,根据等腰三角形的性质证明.
CE,根据等腰三角形的性质证明.
(1)证明:连接OA,
由圆周角定理得,∠ACB=∠ADB,
∵∠ADE=∠ACB,
∴∠ADE=∠ADB,
∵BD是直径,
∴∠DAB=∠DAE=90°,
在△DAB和△DAE中,
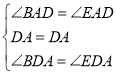 ,
,
∴△DAB≌△DAE,
∴AB=AE,又∵OB=OD,
∴OA∥DE,又∵AH⊥DE,
∴OA⊥AH,
∴AH是⊙O的切线;
(2)解:由(1)知,∠E=∠DBE,∠DBE=∠ACD,
∴∠E=∠ACD,
∴AE=AC=AB=6.
在Rt△ABD中,AB=6,BD=8,∠ADE=∠ACB,
∴sin∠ADB=![]() =
=![]() ,即sin∠ACB=
,即sin∠ACB=![]() ;
;
(3)证明:由(2)知,OA是△BDE的中位线,
∴OA∥DE,OA=![]() DE.
DE.
∴△CDF∽△AOF,
∴![]() =
=![]() ,
,
∴CD=![]() OA=
OA=![]() DE,即CD=
DE,即CD=![]() CE,
CE,
∵AC=AE,AH⊥CE,
∴CH=HE=![]() CE,
CE,
∴CD=![]() CH,
CH,
∴CD=DH.


科目:初中数学 来源: 题型:
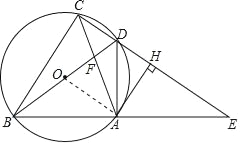
【题目】如图,在△ABC中,AB=AC,以AC为直径做⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)填空:当EF=4,![]() 时,则DE的长为 .
时,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.
厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数,2、结合转盘简述获奖方式,不需说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=ax2+bx+c(a、b、c为常数,且a≠0)时,甲发现当x=1时,函数有最大值;乙发现﹣1是方程ax2+bx+c=0的一个根;丙发现函数的最大值为﹣1;丁发现当x=2时,y=﹣2,已知四位中只有一位发现的结论时错误的,则该同学是( ).
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP= 时,四边形AOCP是菱形;
②连接BP,当∠ABP= 时,PC是⊙O的切线.
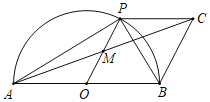
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2019的坐标为( )
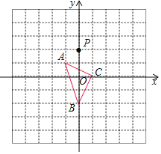
A.(-2,0)B.![]() C.(2,-4)D.(-2,-2)
C.(2,-4)D.(-2,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.
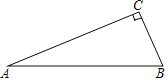
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com