
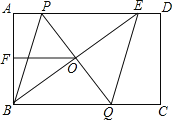
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:△BOQ≌△EOP;
(2)求证:四边形BPEQ是菱形;
(3)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
【答案】(1)见解析;(2)见解析;(3)PQ=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP;
(2)由(1)得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论;
(3)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18-x,在Rt△ABE中,根据勾股定理可得62+x2=(18-x)2,BE=10,得到OB=![]() BE=5,设PE=y,则AP=8-y,BP=PE=y,在Rt△ABP中,根据勾股定理可得62+(8-y)2=y2,解得y=
BE=5,设PE=y,则AP=8-y,BP=PE=y,在Rt△ABP中,根据勾股定理可得62+(8-y)2=y2,解得y=![]() ,在Rt△BOP中,根据勾股定理可得PO=
,在Rt△BOP中,根据勾股定理可得PO=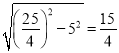 ,由PQ=2PO即可求解.
,由PQ=2PO即可求解.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
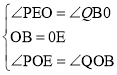 ,
,
∴△BOQ≌△EOP(ASA),
(2)∵△BOQ≌△EOP
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(3)解:∵O,F分别为PQ,AB的中点,
∴AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴OB=![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ABP中,62+(8﹣y)2=y2,解得y=![]() ,
,
在Rt△BOP中,PO=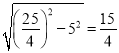 ,
,
∴PQ=2PO=![]() .
.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
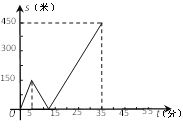
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
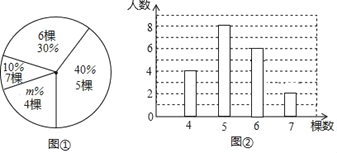
【题目】某校260名学生参加植树活动,活动结束后学校随机调查了部分学生每人的植树棵数,并绘制成如下的统计图①和统计图②.请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为______,图①中m的值为_______;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)求本次调查获取的样本数据的平均数,并根据样本数据,估计这260名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
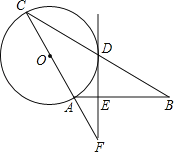
【题目】如图,在△ABC中,AB=AC,以AC为直径做⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)填空:当EF=4,![]() 时,则DE的长为 .
时,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 甲、乙两名同学参加少年科技创新选拔赛,六次比赛的成绩如下:
甲:87 93 88 93 89 90
乙:85 90 90 96 89 a
(1)甲同学成绩的中位数是 ;
(2)若甲、乙的平均成绩相同,则a= ;
(3)已知乙的方差是![]() ,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.(方差公式:S2=
,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.(方差公式:S2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.
厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数,2、结合转盘简述获奖方式,不需说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com