练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，AB=4，AD=7，其中点E为CD的中点．有一动点P，从点A按A→B→C→E的顺序在矩形ABCD的边上移动，移动到点E停止，在此过程中以点A，P，E三点为顶点的直角三角形的个数为（ ）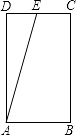

    A.2
    B.3
    C.4
    D.5

    【答案】B
    【解析】解：如图，有三个直角三角形：

    ①当P在AB的中点时，∠AP1E=90°；

    ②以AE为直径的圆与BC有两个交点，则∠AP2E=∠AP3E=90°；

    所以答案是：B．

    【考点精析】本题主要考查了矩形的性质和圆周角定理的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠A=∠C=90°，BE、DF分别平分∠ABC、∠ADC，判断BE、DF是否平行，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八（1）班同学为了解2018年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：

    （1）本次调查采用的调查方式是________（填“普查”或“抽样调查”），样本容量是________；

    （2）补全频数分布直方图：

    （3）若将月均用水量的频数绘成扇形统计图，则月均用水量“”的圆心角度数是________；

    （4）若该小区有5000户家庭，求该小区月均用水量超过的家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，C(0，5)，D(a，5)（a ＞0），A、B 在 x 轴上，∠1=∠D，求证：∠ACB+∠BED=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A（3，3），B（5，3）．

    （1）已知点C（2，－4），求四边形AOCB的面积；

    （2）将线段OB先向上平移2个单位长度，再向左平移4个单位长度，得到线段O2B2，画出两次平移后的图形，并求线段OB在两次平移过程中扫过的总面积．

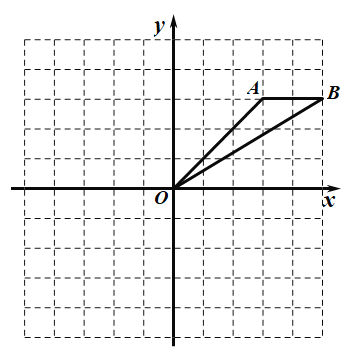
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】推理填空：如图，E点为DF上的点，B为AC上的点， ，那么，请完成它成立的理由

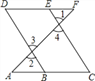
    解： ______

    又

    ______

    ______ ______ ______

    ______

    ______

    ______

    ______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题:求下列事件概率
    （1）小杨和小姜住在同一个小区，该小区到苏果超市有A、B、C三条路线．
    ①求小杨随机选择一条路线，恰好是A路线的概率；
    ②求小杨和小姜两人分别随机选择一条路线去苏果超市，恰好两人选择同一条路线的概率．
    （2）有4位顾客在超市中选购4种品牌的方便面．如果每位顾客从4种品牌中随机的选购一种，那么4位顾客选购同一品牌的概率是 ， 至少有2位顾客选择的不是同一品牌的概率是（直接填字母序号）
    A． B．（ ）3 C．1﹣（ ）3 D．1﹣（ ）3 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题探究】
    已知：如图①所示，∠MPN的顶点为P，⊙O的圆心O从顶点P出发，沿着PN方向平移．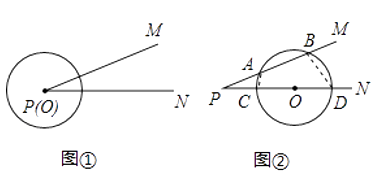

    （1）如图②所示，当⊙O分别与射线PM，PN相交于A、B、C、D四个点，连接AC、BD，可以证得△PAC∽△ ， 从而可以得到：PAP B=P CP D．
    （2）如图③所示，当⊙O与射线PM相切于点A，与射线PN相交于C、D两个点．求证：PA2=PCPD．

    （3）【简单应用】
    如图④所示，（2）中条件不变，经过点P的另一条射线与⊙O相交于E、F两点．利用上述（1），（2）两问的结论，直接写出线段PA与PE、PF之间的数量关系；当PA=4 ，EF=2，则PE= ．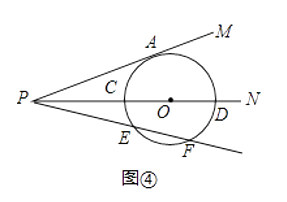

    （4）【拓展延伸】如图⑤所示，在以O为圆心的两个同心圆中，A、B是大⊙O上的任意两点，经过A、B 两点作线段，分别交小⊙O于C、E、D、F四个点．求证：ACAE=BDBF．（友情提醒：可直接运用本题上面所得到的相关结论）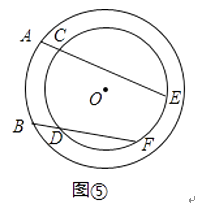

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．

    （1）求∠CBE的度数；

    （2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．

    查看答案和解析>>

    同步练习册答案