
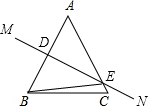
 解:(1)当AB的中垂线MN与AC边相交时,
解:(1)当AB的中垂线MN与AC边相交时,| 1 |
| 2 |
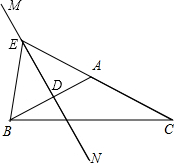 ∴∠EBC=∠ABC-∠ABE=15°;
∴∠EBC=∠ABC-∠ABE=15°;| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 6 |
| 3 |
| 8 |
| 1 |
| 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直 |
| B、从直线外一点到这条直线的垂线段叫做点到直线的距离 |
| C、一条直线的垂线可以画无数条 |
| D、连接直线外一点与直线上各点的所有线段中,垂线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.
如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com